/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2024
Egzamin Ósmoklasisty
z Matematyki (termin dodatkowy) 11 czerwca 2024 Czas pracy: 100 minut
Adam zapisał, w przypadkowej kolejności, podane w programie radiowym wartości temperatury odnotowane pewnego zimowego dnia o godzinie 20:30 w Zakopanem, w Wiśle, w Karpaczu i w Szklarskiej Porębie (zobacz rysunek).
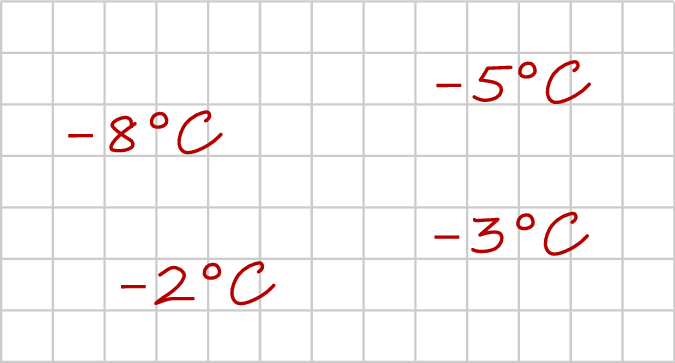
Temperatura w Karpaczu była o 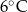 wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę
wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę 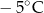 zanotowano w
zanotowano w
A) Szklarskiej Porębie. B) Zakopanem. C) Karpaczu. D) Wiśle.
Dane są cztery liczby:
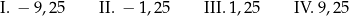
Do której z liczb I–IV należy dodać liczbę 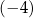 , aby otrzymać liczbę
, aby otrzymać liczbę 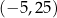 ?
?
A) I B) II C) III D) IV
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
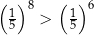 | P | F |
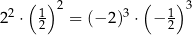 | P | F |
W pudełku są kulki czerwone, zielone i niebieskie. Kulek czerwonych jest trzy razy więcej niż zielonych i o dwie mniej niż niebieskich. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W pudełku najmniej jest kulek A/B .
A) niebieskich B) zielonych
Jeśli liczbę kulek zielonych oznaczymy przez  , to liczbę wszystkich kulek w pudełku opisuje wyrażenie C/D .
, to liczbę wszystkich kulek w pudełku opisuje wyrażenie C/D .
C) 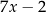 D)
D) 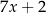
Na osi liczbowej zaznaczono sześć liczb całkowitych. Cztery z tych liczb oznaczono literami: 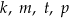 .
.

Które z poniższych wyrażeń ma wartość równą 1?
A) 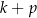 B)
B) 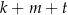 C)
C) 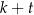 D)
D) 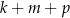
Czy liczba 27 733 jest podzielna przez 3?
Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | cyfrą jedności tej liczby jest 3. |
| B) | suma cyfr tej liczby nie jest podzielna przez 3. |
| C) | dwie ostatnie cyfry tej liczby tworzą liczbę podzielną przez 3. |
Kąty 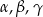 pewnego trójkąta spełniają dwa warunki:
pewnego trójkąta spełniają dwa warunki: 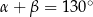 i
i 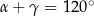 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt  ma miarę ma miarę 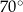 . . | P | F |
Różnica miar między kątem największym a kątem najmniejszym w tym trójkącie jest równa 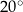 . . | P | F |
W pewnym opakowaniu są płatki owsiane z rodzynkami. Masa zawartości tego opakowania jest równa 320 g, przy czym 15% tej masy stanowią rodzynki. Ola zmieszała całą zawartość tego opakowania z 80 g orzechów.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W mieszance przygotowanej przez Olę masa orzechów jest większa o A/B od masy rodzynek.
A) 32 g B) 48 g
Mieszanka przygotowana przez Olę zawiera C/D orzechów.
C) 20% D) 25%
Antek jest zawodnikiem szkolnej drużyny koszykówki. Od początku sezonu jego drużyna zagrała w sześciu meczach. Antek w tych sześciu meczach zdobył łącznie 84 punkty.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia liczby punktów zdobytych przez Antka w jednym meczu jest równa 14. | P | F |
| Średnia liczby punktów zdobytych przez Antka w jednym meczu będzie równa 15, jeśli w siódmym meczu zdobędzie on 21 punktów. | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba 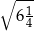 jest równa A/B .
jest równa A/B .
A) 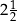 B)
B) 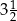
Liczba 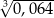 jest równa C/D .
jest równa C/D .
C) 0,4 D) 0,8
W układzie współrzędnych 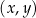 narysowano trapez
narysowano trapez 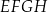 . Wszystkie współrzędne wierzchołków
. Wszystkie współrzędne wierzchołków 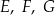 i
i 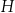 są liczbami całkowitymi.
są liczbami całkowitymi.
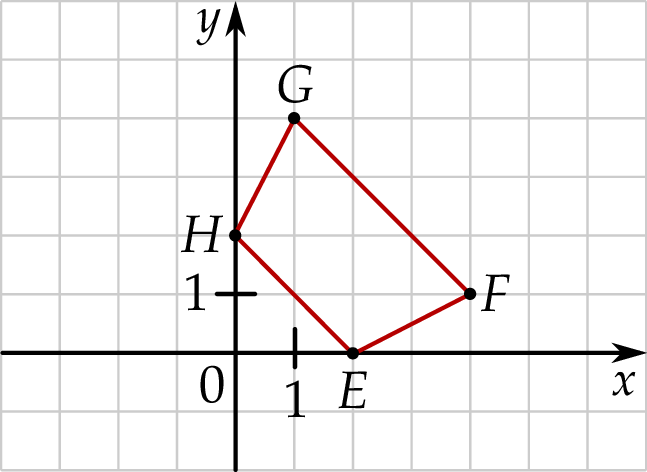
Punkty o współrzędnych 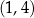 i
i 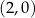 to wierzchołki
to wierzchołki
A) 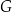 i
i 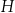 B)
B) 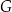 i
i 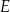 C)
C) 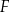 i
i 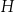 D)
D) 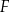 i
i 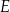
Na planie miasta wykonanym w skali 1:5000 odległość w linii prostej między punktem oznaczającym wejście do papugarni a punktem oznaczającym wejście do muzeum zabawek jest równa 8,4 cm. W terenie odległość między wejściami do tych obiektów jest w linii prostej równa
A) 4,2 m B) 42 m C) 420 m D) 4200 m
Na rysunku przedstawiono kwadrat podzielony na 6 jednakowych prostokątów. Obwód każdego z tych prostokątów jest równy 28.

Obwód kwadratu jest równy
A) 48 B) 84 C) 96 D) 144
Działka ma powierzchnię 200 arów. Warzywa zajmują 130 arów, jabłonie rosną na 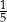 pozostałej części działki, a resztę działki zajmują śliwy. Śliwy zajmują powierzchnię
pozostałej części działki, a resztę działki zajmują śliwy. Śliwy zajmują powierzchnię
A) 14 arów. B) 30 arów. C) 56 arów. D) 70 arów.
W pudełku są klocki w kształcie ostrosłupów trójkątnych i sześcianów. Klocków w kształcie ostrosłupów trójkątnych jest trzy razy więcej niż klocków sześciennych. Wszystkie klocki mają łącznie 720 krawędzi. Ile klocków w kształcie sześcianu jest w tym pudełku?
A) 24 B) 30 C) 39 D) 40
Na diagramie przedstawiono rozkład liczby punktów zdobytych przez zawodników biorących udział w grze Kulki.
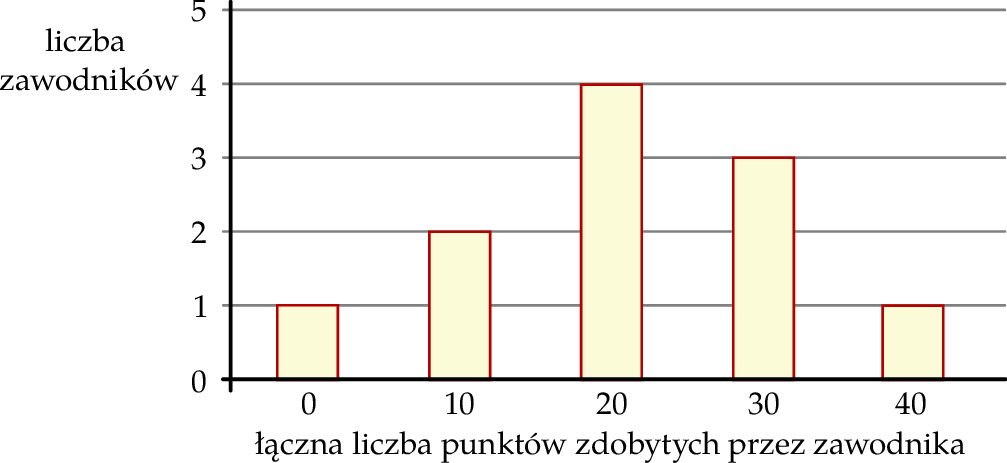
Oblicz prawdopodobieństwo, że losowo wybrany zawodnik zdobył w tej grze więcej niż 20 punktów.
Jednakowe kubki sprzedawane są w dwóch rodzajach opakowań – małych i dużych. W małym opakowaniu jest dwa razy mniej kubków niż w dużym. W dwóch dużych opakowaniach i sześciu małych znajduje się łącznie 140 kubków. Oblicz, ile kubków jest w sześciu dużych opakowaniach.
Na trawniku w kształcie kwadratu o boku długości 9 metrów wytyczono kwietnik w kształcie prostokąta tak, że jego boki są równoległe do boków trawnika. Do kwietnika prowadzą cztery ścieżki. Dwie krótsze ścieżki mają po 1,5 m długości każda, a dwie dłuższe mają po 2,5 m długości każda (zobacz rysunek).
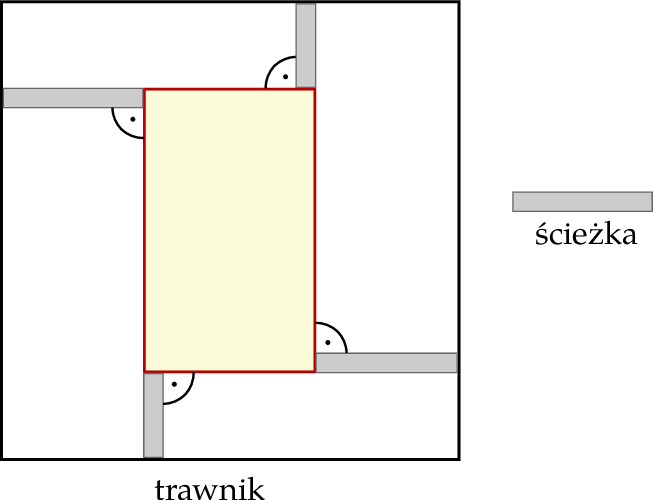
Oblicz pole powierzchni wytyczonego kwietnika.
Dany jest graniastosłup prawidłowy czworokątny, w którym zaznaczone podstawy są kwadratami. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 1. jest równa 27 cm. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 2. jest równa 30 cm.
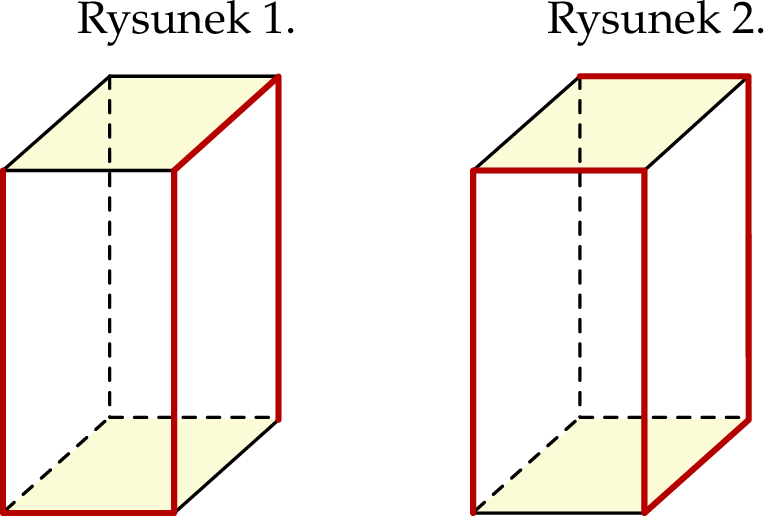
Oblicz objętość tego graniastosłupa.

