/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2024
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 27 kwietnia 2024 Czas pracy: 100 minut
Poniżej przedstawiono składniki potrzebne do przygotowania ciasta na 15 racuchów.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Do przygotowania ciasta na 40 racuchów, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 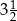 szklanki mąki. szklanki mąki. | P | F |
Do przygotowania ciasta na 54 racuchy, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 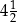 szklanki mleka. szklanki mleka. | P | F |
Córka obecnie jest 3 razy młodsza od swojej mamy. Razem mają 64 lata. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Mama obecnie ma A/B lat.
A) 48 B) 45
Córka za 8 lat będzie miała C/D .
C) 24 lata D) 20 lat
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje tą samą wartość dla 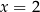 oraz dla
oraz dla 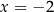 . Które to wyrażenie?
. Które to wyrażenie?
A) 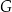 B)
B) 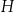 C)
C) 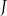 D)
D) 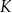
Rozwiązaniem równania
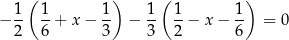
jest liczba
A) 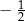 B)
B) 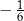 C)
C) 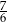 D)
D) 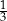 E)
E) 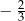
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wyrażenie 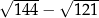 jest równe A/B .
jest równe A/B .
A) 2 B) 1
Wyrażenie 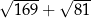 jest równe C/D .
jest równe C/D .
C) 22 D) 23
O godzinie 18:50 Zbyszek wyruszył w podróż pociągiem z Poznania do Legnicy. Najpierw dojechał do Wrocławia, gdzie po 50–minutowym oczekiwaniu wsiadł do pociągu, którym dojechał do Legnicy. Na rysunku pokazano, jak w czasie przebiegała podróż Zbyszka. Na osi czas przejazdu z Poznania do Legnicy podzielono na 22 jednakowe odstępy.
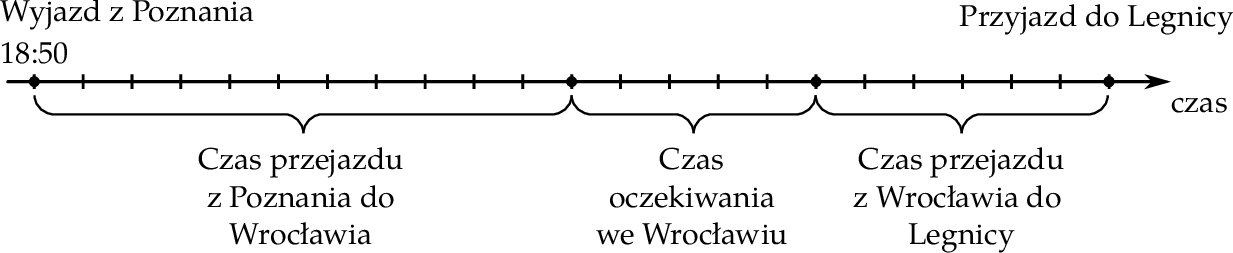
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przejazd z Poznania do Wrocławia trwał dwie godziny. | P | F |
| Zbyszek przyjechał do Legnicy o godzinie 21:30. | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Iloraz 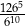 jest równy A/B .
jest równy A/B .
A) 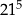 B)
B) 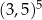
Iloczyn 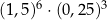 jest równy C/D .
jest równy C/D .
C) 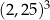 D)
D) 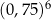
Na tablicy zapisano wszystkie różne liczby trzycyfrowe, które jednocześnie spełniają trzy warunki: są mniejsze od 300, są podzielne przez 18, suma cyfr każdej z nich jest mniejsza od 18. Ile liczb zapisano na tablicy?
A) 9 B) 11 C) 7 D) 6
Pewien ostrosłup ma 17 wierzchołków. Ile wierzchołków ma graniastosłup o takiej samej podstawie, jaką ma ten ostrosłup?
A) 17 B) 30 C) 32 D) 45
Biuro podróży w ramach oferty promocyjnej obniżyło cenę wycieczki o 25%. Pani Anna skorzystała z promocji i za wycieczkę zapłaciła 1800 zł. Jaka była cena wycieczki przed obniżką?
A) 2250 zł. B) 1875 zł. C) 2400 zł. D) 2160 zł.
Z urny, w której są wyłącznie kule białe, czarne i niebieskie losujemy 1 kulę.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli prawdopodobieństwo wylosowania kuli białej jest równe prawdopodobieństwu wylosowania kuli, która nie jest biała, to prawdopodobieństwo wylosowania kuli niebieskiej jest równe  . . | P | F |
Jeżeli prawdopodobieństwo wylosowania kuli białej jest takie samo jak prawdopodobieństwo wylosowania kuli czarnej i jest równe 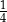 , to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie. , to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie. | P | F |
Dany jest wzór na pole powierzchni trapezu:
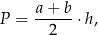
gdzie: 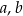 – długości podstaw trapezu,
– długości podstaw trapezu, 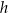 – wysokość trapezu. Długość podstawy
– wysokość trapezu. Długość podstawy  wyznaczona poprawnie z powyższego wzoru opisano równaniem
wyznaczona poprawnie z powyższego wzoru opisano równaniem
A) 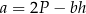 B)
B) 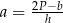 C)
C) 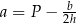 D)
D) 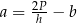
Agata na dużej kartce w kratkę narysowała figurę złożoną z 40 połączonych odcinków, które kolejno ponumerowała liczbami naturalnymi od 1 do 40. Wszystkie komórki kratki są takimi samymi kwadratami. Na rysunku przedstawiono fragment tej figury, złożony z ośmiu początkowych odcinków. Kolejne odcinki tej figury Agata narysowała według tej samej reguły, którą zastosowała do narysowania odcinków 1–8.
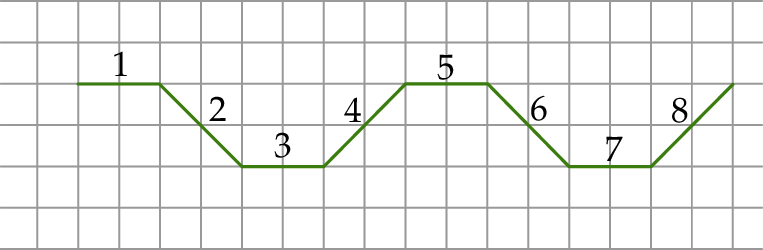
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Proste zawierające odcinki o numerach 2 oraz 8 są wzajemnie prostopadłe. | P | F |
| Proste zawierające odcinki o numerach 5 oraz 32 są wzajemnie równoległe. | P | F |
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 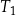 i
i 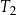 oraz podano długości ich boków.
oraz podano długości ich boków.
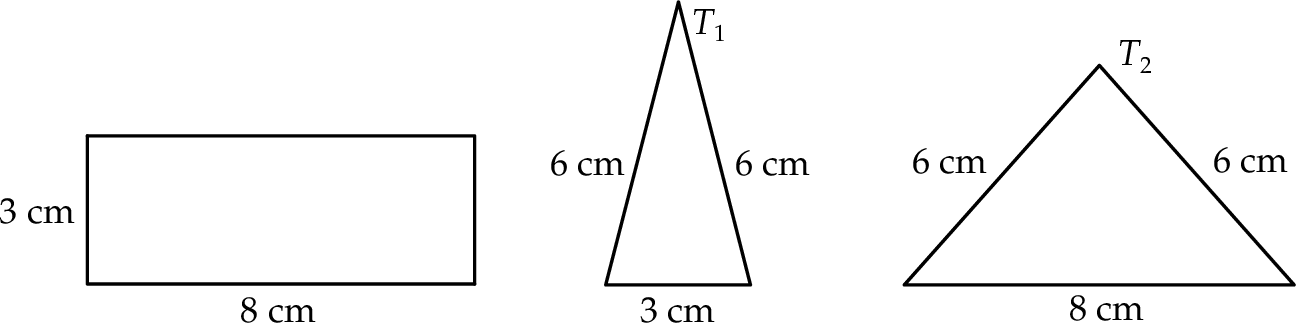
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów 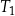 i i 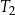 . . |
| B) | trójkąty 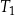 i i 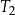 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkątów 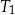 i i 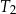 nie są równe długościom boków prostokąta. nie są równe długościom boków prostokąta. |
W czworokącie 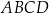 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 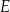 oraz
oraz 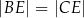 . Przekątna
. Przekątna 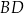 dzieli czworokąt
dzieli czworokąt 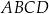 na trójkąt równoboczny i trójkąt równoramienny (zobacz rysunek).
na trójkąt równoboczny i trójkąt równoramienny (zobacz rysunek).
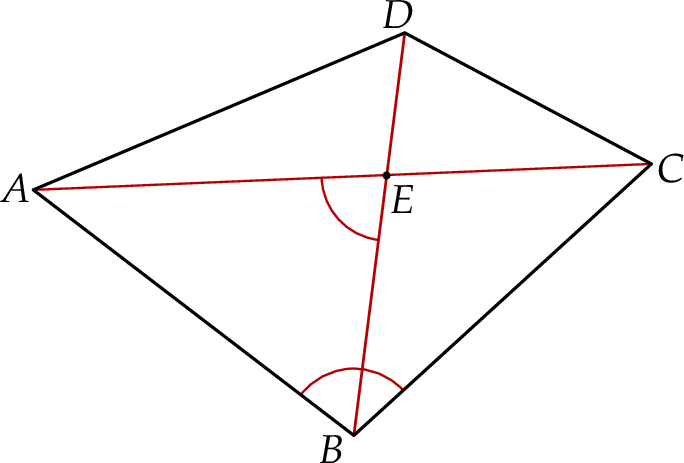
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 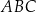 ma miarę ma miarę 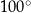 . . | P | F |
Kąt 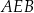 ma miarę ma miarę 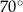 . . | P | F |
Pociąg przebył ze stałą prędkością drogę 900 metrów w czasie 75 sekund. Przy zachowaniu tej samej, stałej prędkości ten sam pociąg drogę równą jego długości przebył w czasie 16 sekund. Oblicz długość tego pociągu.
Prostokątna łąka jest podzielona na dwie części 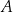 i
i  , tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
, tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
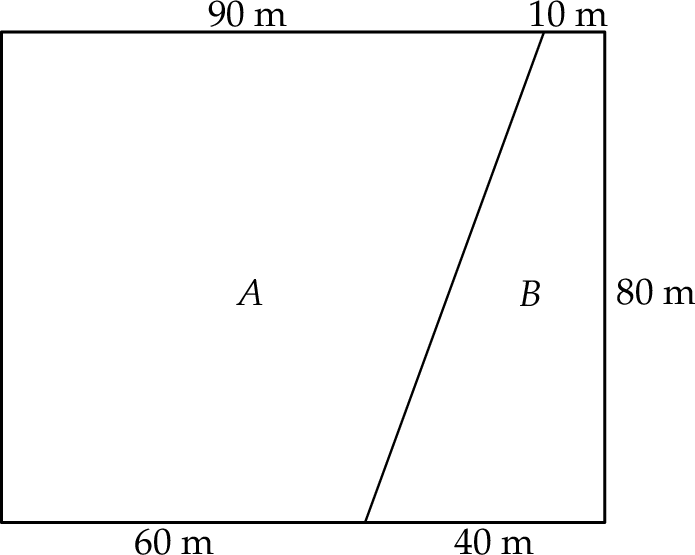
Kosiarka w ciągu każdej godziny swojej pracy kosi trawę z powierzchni o takim samym polu. Trawę z części 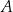 kosiarka skosiła w ciągu sześciu godzin. Oblicz, ile godzin kosiarka będzie kosiła trawę w części
kosiarka skosiła w ciągu sześciu godzin. Oblicz, ile godzin kosiarka będzie kosiła trawę w części 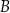 .
.
W kasie są banknoty 10–złotowe, 20–złotowe i 50–złotowe. Liczba banknotów 10–złotowych jest taka sama jak liczba banknotów 50–złotowych i o 32% mniejsza od liczby banknotów 20–złotowych. Łączna wartość wszystkich banknotów 10 i 20–złotowych jest o 540 złotych mniejsza od łącznej wartości wszystkich banknotów 50–złotowych. Oblicz, ile jest wszystkich banknotów w kasie.
Karol ułożył figurę przedstawioną na rysunku. Figura została zbudowana z dwóch rodzajów klocków: sześciennych i prostopadłościennych. Wszystkie klocki tego samego rodzaju mają takie same wymiary.
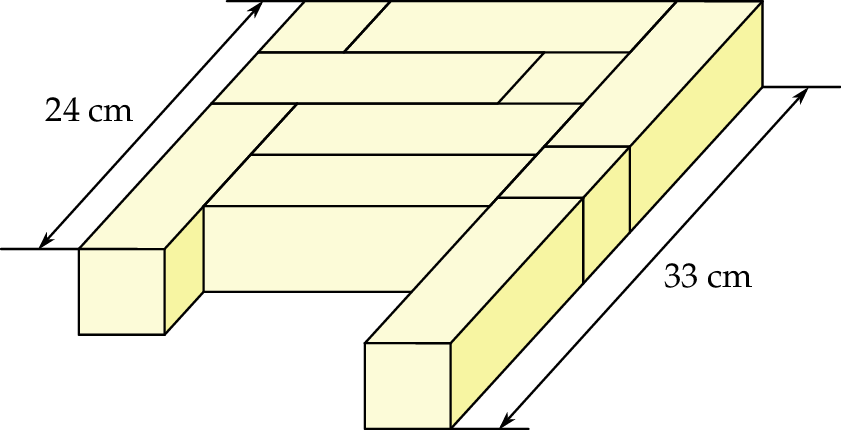
Oblicz objętość bryły zbudowanej z tych klocków.

