/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2024
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 4 maja 2024 Czas pracy: 100 minut
Wśród pewnej grupy osób przeprowadzono ankietę. Jedno z pytań brzmiało: Jaka jest twoja ulubiona pora roku?. Każdy ankietowany wskazał tylko jedną porę roku. Rozkład udzielonych odpowiedzi na to pytanie przedstawiono na diagramie.
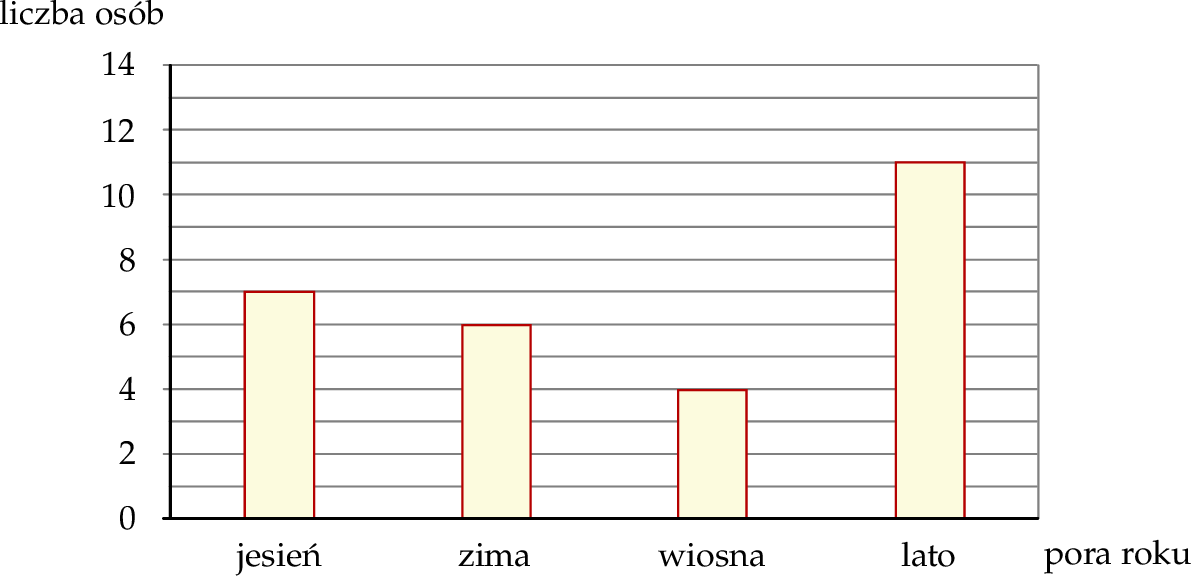
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Zima jest ulubioną porą roku dla więcej niż 20% liczby osób ankietowanych. | P | F |
Wiosna jest ulubioną porą roku dla  liczby osób ankietowanych. liczby osób ankietowanych. | P | F |
Liczba  jest nieparzystą liczbą dwucyfrową, która jest jednocześnie sześcianem liczby naturalnej. Liczba
jest nieparzystą liczbą dwucyfrową, która jest jednocześnie sześcianem liczby naturalnej. Liczba 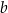 jest dwucyfrową liczbą podzielną przez 12, która jest jednocześnie kwadratem liczby naturalnej. Różnica
jest dwucyfrową liczbą podzielną przez 12, która jest jednocześnie kwadratem liczby naturalnej. Różnica 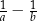 jest równa
jest równa
A) 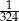 B)
B) 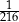 C)
C) 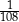 D)
D) 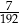
Liczby:  ,
, 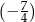 ,
, 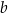 ,
, 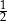 , są uporządkowane rosnąco. Liczba
, są uporządkowane rosnąco. Liczba 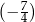 jest większa od liczby
jest większa od liczby  o tyle samo, o ile liczba
o tyle samo, o ile liczba 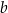 jest większa od liczby
jest większa od liczby 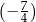 . Liczba
. Liczba  jest większa od liczby
jest większa od liczby 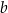 o tyle samo, o ile od liczby
o tyle samo, o ile od liczby  jest większa liczba
jest większa liczba 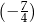 . Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba  jest mniejsza od liczby
jest mniejsza od liczby 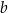 o A/B .
o A/B .
A)  B)
B) 
Liczba 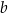 jest mniejsza od liczby
jest mniejsza od liczby 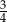 o C/D .
o C/D .
C) 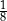 D)
D) 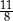
Kamil układa książki na dwóch półkach o tych samych wymiarach wewnętrznych. Wszystkie książki były jednakowych rozmiarów. Pierwszą półkę (I) całkowicie wypełnił 15 książkami. Na drugiej półce (II) postanowił ustawić książki jedna przy drugiej na całej szerokości półki tak, aby zostało nad nimi wolne miejsce, w sposób pokazany na rysunku. Uwaga: na rysunku przedstawiono całkowite wypełnienie książkami pierwszej półki (I) oraz częściowe wypełnienie książkami drugiej półki (II).
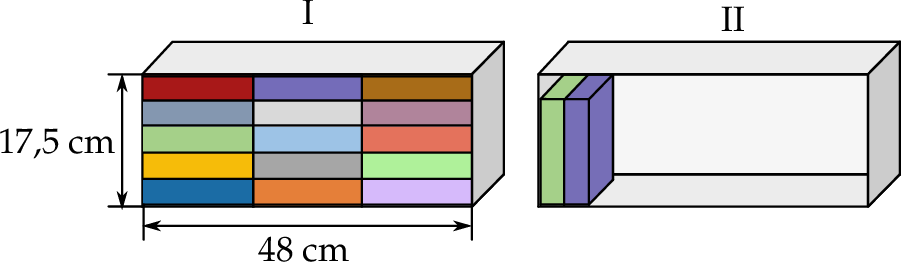
Ile najwięcej książek Kamil mógł zmieścić na drugiej półce (II) przy wskazanym sposobie ustawienia?
A) 12 B) 13 C) 14 D) 15
Dane są trzy liczby:
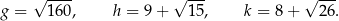
Które spośród tych liczb są mniejsze od liczby 13?
A) Tylko 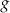 . B) Tylko
. B) Tylko 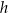 i
i 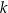 . C) Tylko
. C) Tylko 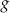 i
i 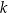 . D) Tylko
. D) Tylko 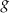 i
i 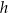 .
.
W zagajniku rosną trzy gatunki drzew: buki, brzozy i świerki. Buków jest o 40% więcej niż brzóz i o 15 więcej niż świerków. Świerków jest o 30% więcej niż brzóz. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W tym zagajniku rośnie ponad 200 buków. | P | F |
| Liczba świerków w tym zagajniku jest o 10% mniejsza od liczby buków. | P | F |
Liczbę 25520 można zapisać w postaci 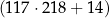 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Reszty z dzielenia liczby 25520 przez 117 i przez 109 są równe. | P | F |
| Reszta z dzielenia połowy liczby 25520 przez 117 jest równa 7. | P | F |
Liczbę  powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę
powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę 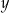 zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
A) 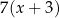 oraz
oraz 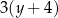 B)
B) 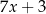 oraz
oraz 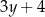
C) 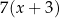 oraz
oraz 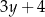 D)
D) 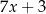 oraz
oraz 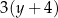
Liczba 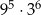 jest równa
jest równa
A) 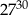 B)
B) 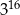 C)
C) 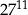 D)
D) 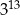
Na planie miasta zaznaczono trasę łączącą dom Marty ze szkołą do której uczęszcza. Trasa ta przebiega obok basenu miejskiego, przy czym odległość z domu do basenu stanowi  trasy z domu do szkoły. Trasa z basenu do szkoły ma długość 800 m.
trasy z domu do szkoły. Trasa z basenu do szkoły ma długość 800 m.
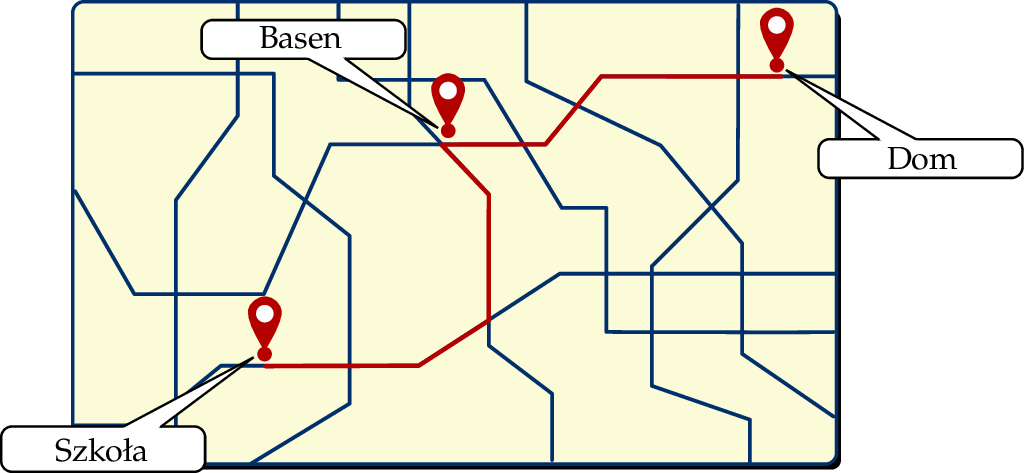
Jaką jest długość całej trasy Marty z domu do szkoły na planie, jeżeli wykonano go w skali 1 : 4 000?
A) 32 cm B) 48 cm C) 0,52 m D) 3,2 m
W pewnym rombie jeden z kątów wewnętrznych ma miarę 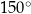 . Pole tego rombu jest równe
. Pole tego rombu jest równe 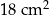 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bok rombu jest dwa razy dłuższy od jego wysokości. | P | F |
| Obwód tego rombu jest równy 27 cm. | P | F |
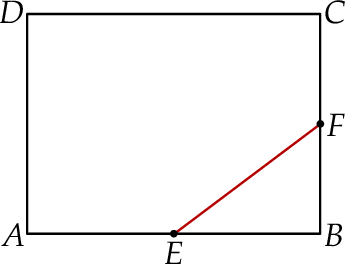
W prostokącie 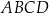 punkty
punkty 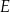 i
i 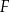 są środkami boków
są środkami boków 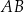 i
i 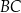 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 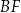 jest równa 9 cm, a długość odcinka
jest równa 9 cm, a długość odcinka 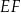 jest równa 15 cm.
jest równa 15 cm.
Obwód prostokąta 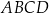 jest równy
jest równy
A) 84 cm B) 96 cm C) 60 cm D) 72 cm
Na rysunku przedstawiono prostokąt 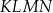 o bokach długości 24 cm i 10 cm.
o bokach długości 24 cm i 10 cm.

Czy wewnątrz tego prostokąta można umieścić odcinek 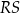 o długości
o długości 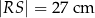 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | długość odcinka 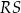 jest większa od długości odcinka jest większa od długości odcinka 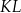 i większa od długości odcinka i większa od długości odcinka 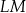 . . |
| B) | suma kwadratów długości odcinków 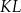 i i 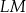 jest mniejsza niż kwadrat długości odcinka jest mniejsza niż kwadrat długości odcinka 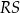 . . |
| C) | suma długości odcinków 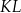 i i 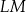 jest większa od długości odcinka jest większa od długości odcinka 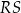 . . |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 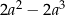 dla
dla 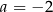 jest równa A/B .
jest równa A/B .
A) 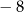 B) 24
B) 24
Wyrażenie 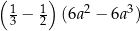 można przekształcić do postaci C/D .
można przekształcić do postaci C/D .
C) 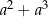 D)
D) 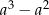
Na rysunku przedstawiono prostokąt. Długość dłuższego boku oznaczono symbolem  oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 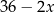 . Długość krótszego boku oznaczono symbolem
. Długość krótszego boku oznaczono symbolem 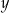 oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 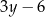 .
.
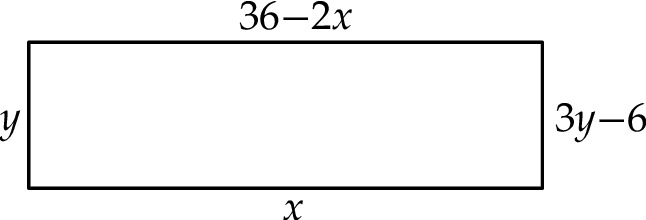
Które równanie nie opisuje poprawnej zależności między wartościami  i
i 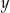 ?
?
A) 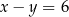 B)
B) 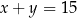 C)
C) 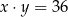 D)
D) 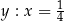
Cena biletu do kina jest o 148 zł mniejsza od ceny biletu do teatru. Za 3 bilety do teatru i 5 biletów do kina zapłacono łącznie 700 zł. Oblicz cenę jednego biletu do kina.
W trapezie prostokątnym 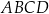 dane są długości podstaw
dane są długości podstaw 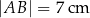 i
i 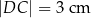 oraz długość ramienia prostopadłego do postaw
oraz długość ramienia prostopadłego do postaw 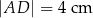 (zobacz rysunek).
(zobacz rysunek).
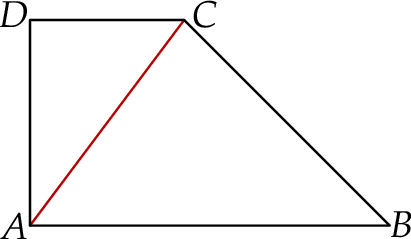
Oblicz odległość punktu 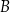 od przekątnej
od przekątnej 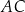 trapezu
trapezu 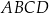 .
.
W pudełku 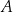 znajdowały się piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich znajdujących się w pudełku
znajdowały się piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich znajdujących się w pudełku 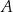 były – odpowiednio – kolejnymi liczbami podzielnymi przez 12. Połowę piłeczek czerwonych, połowę zielonych i połowę niebieskich przełożono do pojemnika
były – odpowiednio – kolejnymi liczbami podzielnymi przez 12. Połowę piłeczek czerwonych, połowę zielonych i połowę niebieskich przełożono do pojemnika 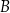 , a wszystkie piłeczki, które pozostały w pojemniku
, a wszystkie piłeczki, które pozostały w pojemniku 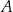 przełożono do pojemnika
przełożono do pojemnika 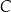 . Następnie, wszystkie piłeczki z pojemnika
. Następnie, wszystkie piłeczki z pojemnika 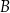 podzielono na 6 identycznych zestawów, a wszystkie piłeczki z pojemnika
podzielono na 6 identycznych zestawów, a wszystkie piłeczki z pojemnika 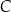 podzielono na 3 identyczne zestawy. Po dokonaniu tego podziału pokazało się, że w każdym zestawie utworzonym z piłeczek w pudełku
podzielono na 3 identyczne zestawy. Po dokonaniu tego podziału pokazało się, że w każdym zestawie utworzonym z piłeczek w pudełku 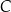 jest o 6 niebieskich piłeczek więcej, niż liczba piłeczek zielonych w zestawie utworzonym z piłeczek z pudełka
jest o 6 niebieskich piłeczek więcej, niż liczba piłeczek zielonych w zestawie utworzonym z piłeczek z pudełka 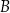 . Ile piłeczek czerwonych było początkowo w pudełku
. Ile piłeczek czerwonych było początkowo w pudełku 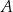 ?
?
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa 12 cm, a długość przeciwprostokątnej jest równa 15 cm. Najmniejsza ściana boczna tego graniastosłupa ma pole równe 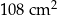 .
.

Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.

