/Szkoła średnia/Zadania maturalne/Matura 2024/Matura
Egzamin Maturalny
z Matematyki (termin dodatkowy)]
formuła 2015
poziom podstawowy 4 czerwca 2024 Czas pracy: 170 minut
Zadania zamknięte
Liczba 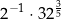 jest równa
jest równa
A) 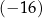 B)
B) 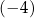 C) 2 D) 4
C) 2 D) 4
Liczba 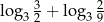 jest równa
jest równa
A) 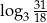 B)
B) 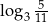 C)
C) 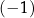 D)
D) 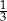
Liczba 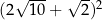 jest równa
jest równa
A) 22 B) 42 C) 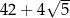 D)
D) 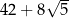
Dane są dwa prostokąty:  oraz
oraz 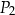 . Długości boków prostokąta
. Długości boków prostokąta 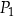 są równe
są równe  oraz
oraz 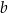 . Długości boków prostokąta
. Długości boków prostokąta 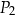 są równe
są równe 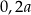 oraz
oraz 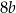 . Pole prostokąta
. Pole prostokąta 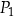 stanowi
stanowi
A) 60% pola prostokąta 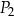 .
.
B) 62,5% pola prostokąta 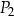 .
.
C) 160% pola prostokąta 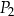 .
.
D) 162,5% pola prostokąta 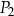 .
.
Klient wpłacił do banku na trzyletnią lokatę kwotę w wysokości 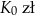 . Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 6% od kwoty bieżącego kapitału znajdującego się na lokacie – zgodnie z procentem składanym. Po trzech latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 6% od kwoty bieżącego kapitału znajdującego się na lokacie – zgodnie z procentem składanym. Po trzech latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
A) 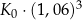 B)
B) 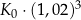 C)
C) 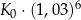 D)
D) 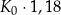
Liczba wszystkich całkowitych dodatnich rozwiązań nierówności
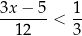
jest równa
A) 2 B) 3 C) 5 D) 6
Układ równań 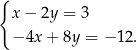
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Jednym z rozwiązań równania 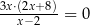 jest liczba
jest liczba
A) 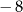 B)
B) 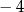 C) 2 D) 3
C) 2 D) 3
Funkcja 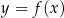 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 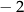 | 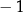 | 0 | 1 | 2 |
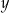 | 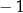 | 0 | 1 | 0 | 3 |
Wskaż zdanie prawdziwe.
A) Funkcja 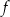 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
B) W układzie współrzędnych 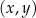 wykres funkcji
wykres funkcji 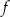 jest symetryczny względem osi
jest symetryczny względem osi 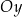 .
.
C) Największa wartość funkcji 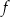 jest równa 3.
jest równa 3.
D) Najmniejsza wartość funkcji 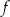 jest równa
jest równa 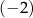 .
.
Liczba 2 jest miejscem zerowym funkcji liniowej 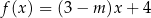 . Liczba
. Liczba 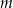 jest równa
jest równa
A) 0 B) 3 C) 4 D) 5
Informacja do zadań 11 – 13
Na rysunku, w układzie współrzędnych  , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 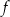 .
.
Największa wartość funkcji  jest równa
jest równa
A) 2 B) 4 C) 6 D) 7
Funkcja  jest malejąca w zbiorze
jest malejąca w zbiorze
A) ![[− 1,1]](https://img.zadania.info/zes/0085867/HzesT54x.png) B)
B) ![[0 ,4]](https://img.zadania.info/zes/0085867/HzesT55x.png) C)
C) ![[1,7]](https://img.zadania.info/zes/0085867/HzesT56x.png) D)
D) ![[4,7]](https://img.zadania.info/zes/0085867/HzesT57x.png)
Na drugim rysunku przedstawiono wykres funkcji 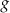 , powstałej w wyniku przesunięcia równoległego wykresu funkcji
, powstałej w wyniku przesunięcia równoległego wykresu funkcji 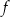 wzdłuż osi
wzdłuż osi 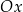 o 4 jednostki w lewo.
o 4 jednostki w lewo.
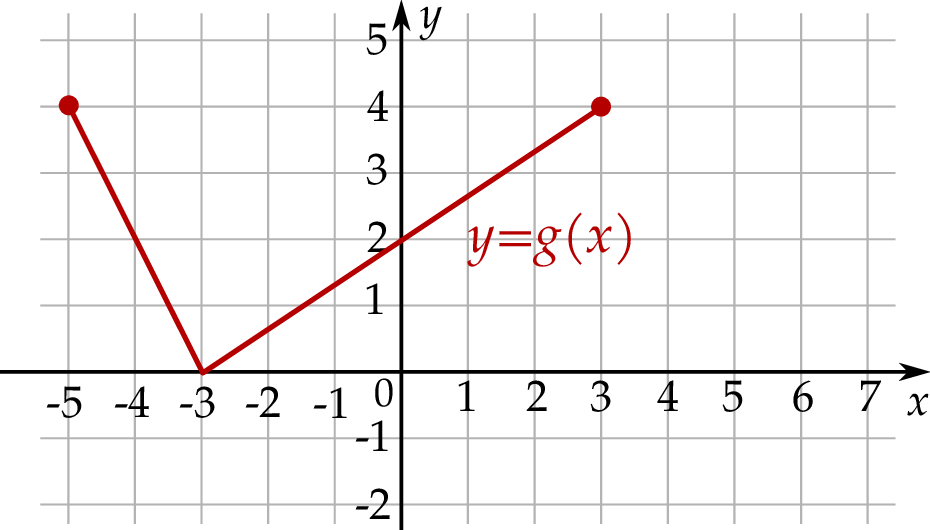
Funkcje 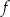 i
i 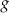 są powiązane zależnością
są powiązane zależnością
A) 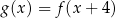 B)
B) 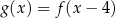
C) 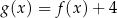 D)
D) 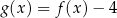
Funkcja kwadratowa 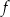 jest określona wzorem
jest określona wzorem 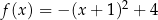 . Fragment wykresu funkcji
. Fragment wykresu funkcji 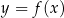 przedstawiono na rysunku
przedstawiono na rysunku
Ciąg  jest określony wzorem
jest określony wzorem 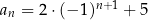 dla każdej liczby naturalnej
dla każdej liczby naturalnej 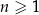 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 3 B) 7 C) 50 D) 100
W ciągu arytmetycznym 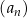 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 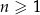 , dane są wyrazy:
, dane są wyrazy: 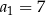 oraz
oraz 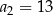 . Wyraz
. Wyraz 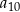 jest równy
jest równy
A) 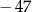 B) 52 C) 61 D) 67
B) 52 C) 61 D) 67
Trzywyrazowy ciąg 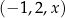 jest arytmetyczny. Trzywyrazowy ciąg
jest arytmetyczny. Trzywyrazowy ciąg 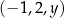 jest geometryczny. Liczby
jest geometryczny. Liczby  oraz
oraz  spełniają warunki
spełniają warunki
A)  i
i  B)
B) 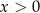 i
i 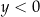 C)
C) 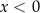 i
i 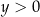 D)
D) 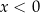 i
i 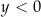
Liczba 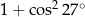 jest równa
jest równa
A)  B)
B) 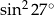 C)
C)  D) 2
D) 2
Podstawy trapezu prostokątnego 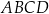 mają długości:
mają długości: 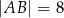 oraz
oraz 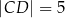 . Wysokość
. Wysokość 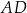 tego trapezu ma długość
tego trapezu ma długość 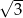 .
.
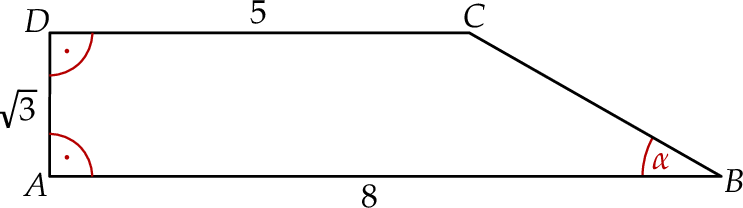
Miara kąta ostrego 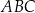 jest równa
jest równa
A) 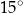 B)
B) 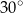 C)
C) 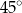 D)
D) 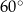
Punkty 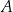 ,
, 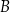 oraz
oraz 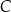 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 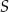 . Długość łuku
. Długość łuku 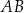 , na którym jest oparty kąt wpisany
, na którym jest oparty kąt wpisany 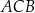 , jest równa
, jest równa 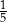 długości okręgu.
długości okręgu.

Miara kąta ostrego 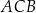 jest równa
jest równa
A) 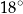 B)
B) 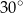 C)
C) 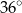 D)
D) 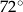
Proste 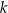 oraz
oraz 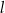 są określone równaniami
są określone równaniami
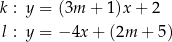
Proste 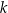 oraz
oraz 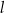 są równoległe, gdy liczba
są równoległe, gdy liczba 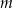 jest równa
jest równa
A) 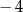 B)
B) 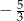 C)
C) 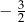 D)
D) 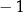
Dana jest prosta o równaniu 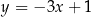 . Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
. Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
A) 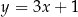 B)
B) 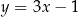 C)
C) 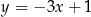 D)
D) 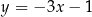
Przekątna ściany sześcianu ma długość 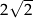 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 8 B) 24 C) 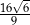 D)
D) 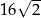
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4. Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 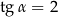 .
.
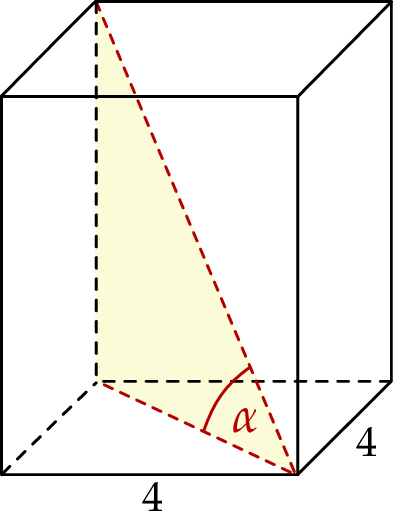
Wysokość tego graniastosłupa jest równa
A) 2 B) 8 C) 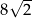 D)
D) 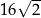
Ostrosłup prawidłowy ma 2024 ściany boczne. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 2025 B) 2026 C) 4048 D) 4052
Dany jest ostrosłup prawidłowy czworokątny 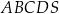 o podstawie
o podstawie 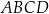 . Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka
. Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka 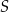 do krawędzi podstawy
do krawędzi podstawy 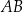 tego ostrosłupa jest równa
tego ostrosłupa jest równa
A) 3 B)  C)
C) 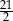 D) 5
D) 5
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę.
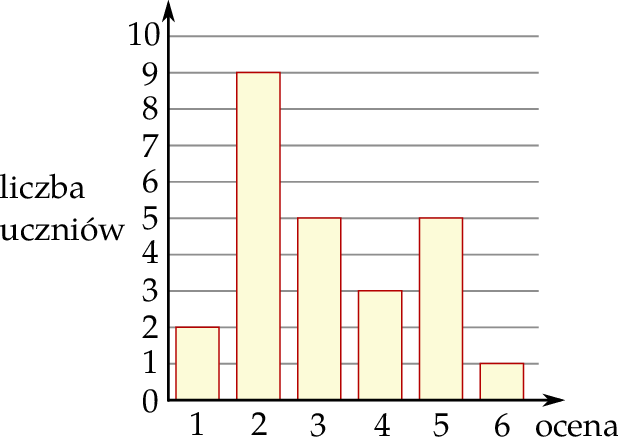
Średnia arytmetyczna ocen uzyskanych z tego sprawdzianu przez uczniów tej klasy jest równa
A) 3 B) 3,12 C) 3,5 D) 4,1(6)
Wszystkich liczb naturalnych czterocyfrowych parzystych, w których zapisie dziesiętnym występują tylko cyfry 2, 4, 7 (np.: 7272, 2222, 7244), jest
A) 16 B) 27 C) 54 D) 81
W pudełku znajdują się wyłącznie kule białe i czarne. Kul czarnych jest 18. Z tego pudełka w sposób losowy wyciągamy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kulę czarną, jest równe  . Liczba kul białych w pudełku, przed wyciągnięciem jednej kuli, była równa
. Liczba kul białych w pudełku, przed wyciągnięciem jednej kuli, była równa
A) 9 B) 12 C) 15 D) 30
Zadania otwarte
Rozwiąż nierówność 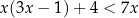 .
.
Parabola, która jest wykresem funkcji kwadratowej 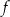 , ma z osiami kartezjańskiego układu współrzędnych
, ma z osiami kartezjańskiego układu współrzędnych 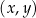 dokładnie dwa punkty wspólne:
dokładnie dwa punkty wspólne: 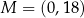 oraz
oraz 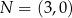 . Wyznacz wzór funkcji kwadratowej
. Wyznacz wzór funkcji kwadratowej 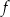 .
.
Wykaż, że dla każdej liczby rzeczywistej 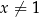 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 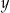 prawdziwa jest nierówność
prawdziwa jest nierówność
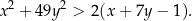
Bok kwadratu 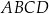 ma długość równą 12. Punkt
ma długość równą 12. Punkt 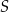 jest środkiem boku
jest środkiem boku 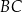 tego kwadratu. Na odcinku
tego kwadratu. Na odcinku 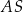 leży punkt
leży punkt 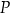 taki, że odcinek
taki, że odcinek 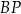 jest prostopadły do odcinka
jest prostopadły do odcinka 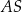 . Oblicz długość odcinka
. Oblicz długość odcinka 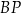 .
.
Trzywyrazowy ciąg 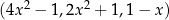 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 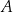 polegającego na tym, że w pierwszym rzucie wypadnie większa liczba oczek niż w drugim rzucie.
polegającego na tym, że w pierwszym rzucie wypadnie większa liczba oczek niż w drugim rzucie.
W kartezjańskim układzie współrzędnych 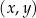 dane są punkty
dane są punkty 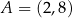 oraz
oraz 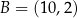 . Symetralna odcinka
. Symetralna odcinka 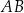 przecina oś
przecina oś 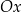 układu współrzędnych w punkcie
układu współrzędnych w punkcie 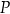 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 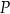 oraz długość odcinka
oraz długość odcinka 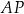 .
.

