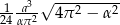/Szkoła średnia/Geometria/Stereometria/Stożek/Objętość

Zadanie nr 2704574

Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym α . Kąt ten oparty jest na łuku długości a . Oblicz objętość stożka.

Wersja PDF

Rozwiązanie

Narysujmy stożek i jego rozwinięcie.

PIC

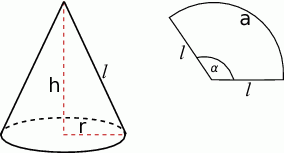
Mamy

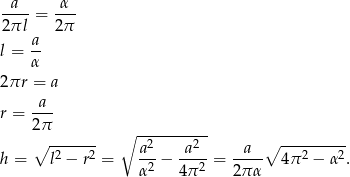
a α ---- = --- 2πl 2π l = a- α 2πr = a a r = --- 2 π ∘ ---------- ∘ -2---2- a2- -a2- -a--∘ ---2----2 h = l − r = α2 − 4 π2 = 2π α 4 π − α .

Pozostało policzyć szukaną objętość

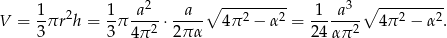
1- 2 1- -a2- --a-∘ ---2----2 -1--a3-∘ ---2----2 V = 3πr h = 3π 4 π2 ⋅2π α 4π − α = 24 απ 2 4π − α .

 
Odpowiedź: 1 a3 √ --------- 24 απ-2 4π 2 − α 2

Wersja PDF