/Szkoła średnia/Geometria/Stereometria/Stożek/Objętość

Zadanie nr 4907758

Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz stosunek objętości stożka do objętości wpisanej w niego kuli.

Wersja PDF

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

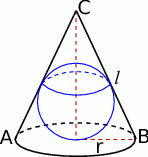
Z podanej informacji mamy równość

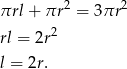
2 2 πrl + πr = 3πr rl = 2r2 l = 2r.

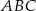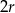W takim razie trójkąt ABC jest równoboczny i promień kuli wpisanej w stożek to dokładnie promień x okręgu wpisanego w trójkąt równoboczny o boku 2r . Mamy więc (ze wzoru na wysokość w trójkącie równobocznym)

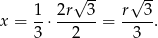
√ -- √ -- 1 2r 3 r 3 x = --⋅------= ----. 3 2 3

Szukany stosunek objętości jest więc równy

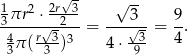
√- 1 2 2r-3 √ -- -3πr--⋅√--2- = ---3√--= 9. 4π (r-3-)3 4⋅ -3- 4 3 3 9

 
Odpowiedź: 9 4

Wersja PDF