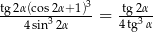Zadanie nr 6727713
W stożek w którym kąt między tworzącą, a podstawą ma miarę 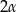 wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli.
wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli.
Rozwiązanie
Zaczynamy oczywiście od rysunku. Od razu narysujmy sobie przekrój opisanej sytuacji.
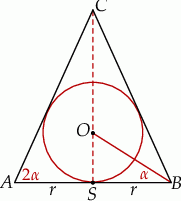
Musimy jakoś wyznaczyć promień okręgu wpisanego w trójkąt 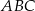 . Zrobimy to na dwa sposoby, ale wcześniej zauważmy, że mamy równości
. Zrobimy to na dwa sposoby, ale wcześniej zauważmy, że mamy równości
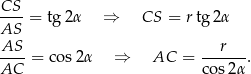
Obliczmy jeszcze objętość stożka (w zależności od  i
i  ).
).
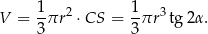
Sposób I
Standardowy sposób wyznaczenia promienia okręgu wpisanego w trójkąt to wzór na pole 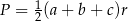 . Żeby nie mylić z promieniem podstawy stożka, oznaczmy promień kuli wpisanej w stożek przez
. Żeby nie mylić z promieniem podstawy stożka, oznaczmy promień kuli wpisanej w stożek przez 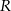 . Mamy zatem
. Mamy zatem
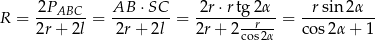
Zatem objetość kuli wynosi
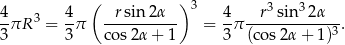
Zatem szukany iloraz jest równy
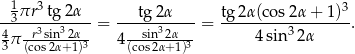
Sposób II
Promień okręgu wpisanego w trójkąt 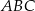 możemy również wyliczyć z trójkąta
możemy również wyliczyć z trójkąta 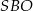 , gdzie
, gdzie 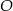 - środek kuli wpisanej w stożek (zatem
- środek kuli wpisanej w stożek (zatem 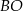 to dwusieczna kąta
to dwusieczna kąta 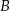 ). Mamy
). Mamy
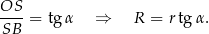
Zatem objętość kuli to
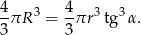
A szukany iloraz to
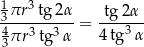
No i mamy dobre ćwiczenie, żeby sprawdzić, że jest to ten sam wynik co poprzednio.
Odpowiedź: