/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2024/Egzamin
Egzamin Ósmoklasisty
z Matematyki 15 maja 2024 Czas pracy: 100 minut
Ala codziennie uczyła się języka hiszpańskiego. Na diagramie przedstawiono, ile czasu przeznaczyła na naukę tego języka w kolejnych dniach tygodnia od poniedziałku do soboty.
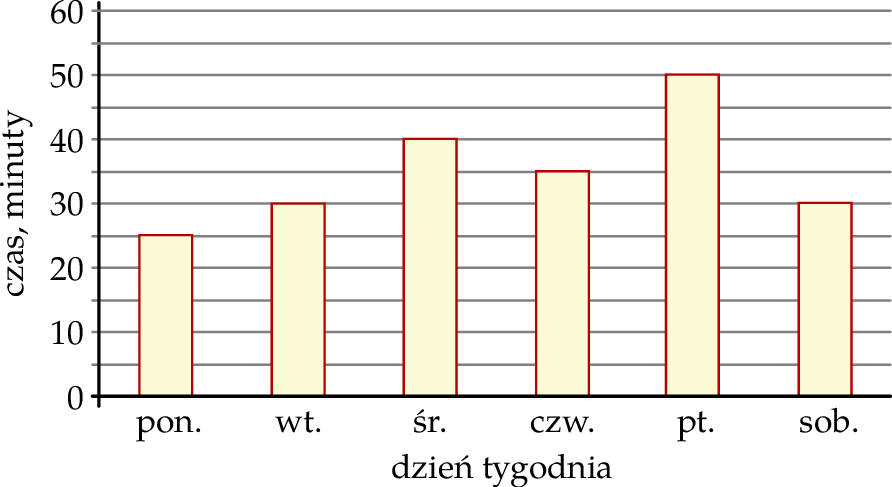
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Ala przez cztery dni – od poniedziałku do czwartku – na naukę języka hiszpańskiego przeznaczyła łącznie 2 godziny i 10 minut. | P | F |
| Na naukę języka hiszpańskiego w sobotę Ala przeznaczyła o 40% czasu mniej niż w piątek. | P | F |
Wypisano ułamki spełniające łącznie następujące warunki:
-
mianownik każdego z nich jest równy 4,
-
licznik każdego z nich jest liczbą naturalną większą od mianownika,
-
każdy z tych ułamków jest większy od liczby 3 oraz mniejszy od liczby 5.
Wszystkich ułamków spełniających powyższe warunki jest
A) sześć B) siedem C) osiem D) dziewięć
Średnia arytmetyczna trzech liczb: 12, 14, 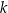 , jest równa 16. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, jest równa 16. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 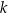 jest równa 22. jest równa 22. | P | F |
Średnia arytmetyczna liczb: 12, 14, 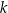 , 11, 17, jest większa od 16. , 11, 17, jest większa od 16. | P | F |
Dane są dwie liczby  i
i 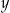 zapisane za pomocą wyrażeń arytmetycznych:
zapisane za pomocą wyrażeń arytmetycznych:
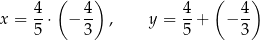
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba 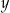 jest liczbą A/B .
jest liczbą A/B .
A) ujemną B) dodatnią
Liczba  jest C/D od liczby
jest C/D od liczby 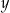 .
.
C) mniejsza D) większa
Dany jest trapez 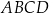 , w którym bok
, w którym bok 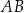 jest równoległy do boku
jest równoległy do boku 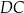 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 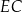 równoległy do boku
równoległy do boku 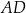 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek).

Kąt  ma miarę
ma miarę
A) 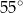 B)
B) 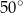 C)
C) 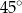 D)
D) 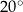
Dane jest równanie
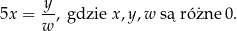
Zadaniem Pawła było przekształcanie tego równania tak, aby wyznaczyć 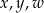 . Paweł otrzymał trzy równania:
. Paweł otrzymał trzy równania:
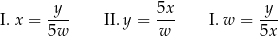
A) I i II B) II i III C) I i III D) I, II, III
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn 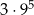 jest równy wartości wyrażenia jest równy wartości wyrażenia 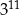 . . | P | F |
Wyrażenie 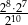 można zapisać w postaci można zapisać w postaci 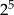 . . | P | F |
Karolina kupiła jedno pudełko balonów. W tabeli podano informacje dotyczące kolorów balonów oraz ich liczby w tym pudełku.

Karolina wyjmowała losowo po jednym balonie z pudełka. Pierwsze dwa wyjęte balony były w kolorze czerwonym. Jakie jest prawdopodobieństwo, że trzeci balon losowo wyjęty przez Karolinę będzie w kolorze czerwonym?
A) 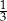 B)
B) 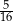 C)
C) 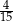 D)
D) 
Wyrażenie 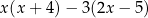 można przekształcić równoważnie do postaci
można przekształcić równoważnie do postaci
A) 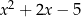 B)
B) 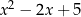 C)
C) 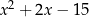 D)
D) 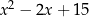
Podróż pociągiem z Olsztyna do Gdyni planowo trwa 2 godziny i 54 minuty. Pewnego dnia pociąg wyjechał z Olsztyna punktualnie o wyznaczonej godzinie, ale przyjechał do Gdyni z czterominutowym opóźnieniem o godzinie 17:31. Pociąg wyjechał z Olsztyna o godzinie
A) 14:27 B) 14:41 C) 14:31 D) 14:33
Na wykresie przedstawiono zależność pola pomalowanej powierzchni od ilości zużytej farby. Pole pomalowanej powierzchni jest wprost proporcjonalne do ilości zużytej farby.
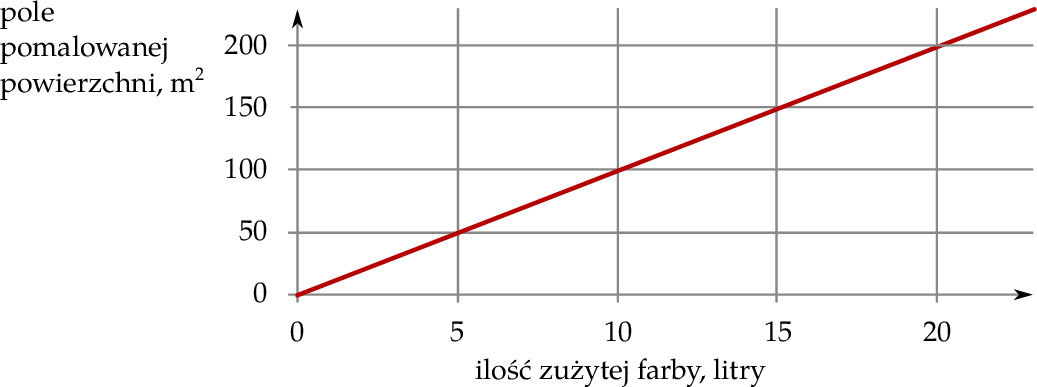
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
18 litrów tej farby wystarczy na pomalowanie 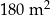 powierzchni. powierzchni. | P | F |
Na pomalowanie 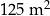 powierzchni wystarczy 12 litrów tej farby. powierzchni wystarczy 12 litrów tej farby. | P | F |
W układzie współrzędnych 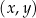 zaznaczono pięć punktów
zaznaczono pięć punktów 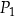 ,
, 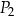 ,
, 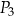 ,
, 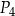 oraz
oraz 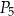 (zobacz rysunek). Wszystkie współrzędne tych punktów są liczbami całkowitymi. Punkt
(zobacz rysunek). Wszystkie współrzędne tych punktów są liczbami całkowitymi. Punkt 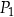 ma współrzędne
ma współrzędne 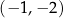 .
.

Jeżeli współrzędną  punktu
punktu 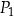 zwiększymy o 4, a współrzędną
zwiększymy o 4, a współrzędną 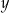 tego punktu zwiększymy o 3, to otrzymamy współrzędne punktu
tego punktu zwiększymy o 3, to otrzymamy współrzędne punktu
A) 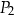 B)
B) 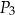 C)
C) 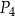 D)
D) 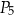
Na rysunku przedstawiono prostokąt o bokach długości  i
i 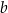 podzielony na sześć kwadratów.
podzielony na sześć kwadratów.
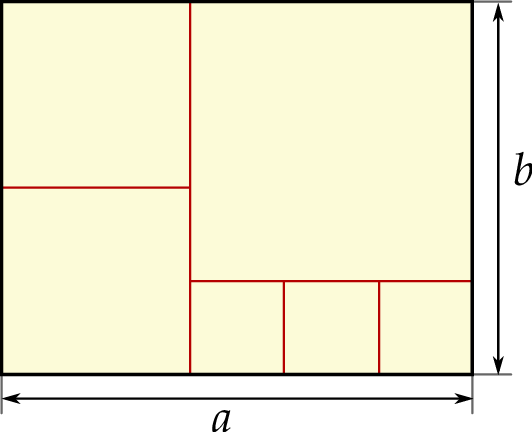
Stosunek długości boków 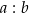 tego prostokąta jest równy
tego prostokąta jest równy
A) 6 : 5 B) 5 : 4 C) 4 : 3 D) 3 : 2
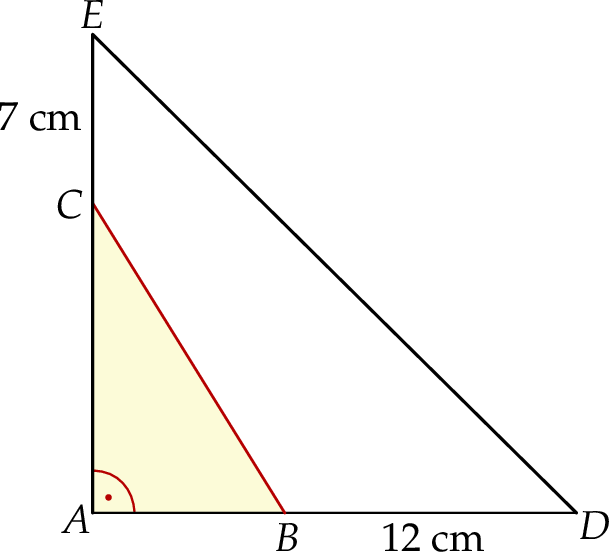
W trójkącie prostokątnym 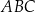 przyprostokątną
przyprostokątną 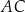 wydłużono o 7 cm, a przyprostokątną
wydłużono o 7 cm, a przyprostokątną 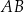 wydłużono o 12 cm i otrzymano trójkąt prostokątny równoramienny
wydłużono o 12 cm i otrzymano trójkąt prostokątny równoramienny 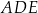 o polu równym
o polu równym 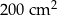 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Przyprostokątna trójkąta 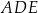 jest równa 20 cm. jest równa 20 cm. | P | F |
Pole trójkąta 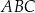 jest równe jest równe 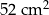 . . | P | F |
Dany jest ostrosłup prawidłowy czworokątny. Pole powierzchni całkowitej tej bryły jest równe 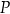 , a jedna ściana boczna ma pole równe
, a jedna ściana boczna ma pole równe 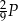 . Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Pole powierzchni bocznej tego ostrosłupa jest równe A/B .
A) 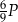 B)
B) 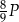
Pole powierzchni podstawy tego ostrosłupa jest dwa razy C/D niż pole powierzchni jego jednej ściany bocznej.
C) mniejsze D) większe
Ela i Ania dostały w prezencie po jednym zestawie puzzli o takiej samej liczbie elementów. Ela ułożyła  swoich puzzli, a Ania
swoich puzzli, a Ania 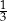 swoich. Dziewczynki ułożyły łącznie 440 elementów. Oblicz, z ilu elementów składa się jeden zestaw puzzli.
swoich. Dziewczynki ułożyły łącznie 440 elementów. Oblicz, z ilu elementów składa się jeden zestaw puzzli.
Prostokąt 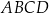 podzielono na trzy trójkąty:
podzielono na trzy trójkąty: 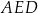 ,
, 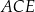 ,
, 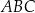 (zobacz rysunek). Na rysunku podano również długości dwóch boków trójkąta
(zobacz rysunek). Na rysunku podano również długości dwóch boków trójkąta 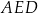 oraz zaznaczono dwa kąty trójkąta
oraz zaznaczono dwa kąty trójkąta 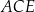 , o takiej samej mierze
, o takiej samej mierze  .
.
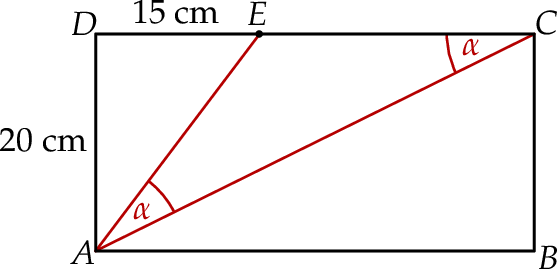
Oblicz pole trapezu 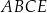 .
.
Pan Jan sprzedał w swoim sklepie 120 kg truskawek. Połowę masy tych truskawek sprzedał w dużych opakowaniach, 10% masy truskawek – w średnich, a pozostałe truskawki w małych opakowaniach. W tabeli podano informacje dotyczące sprzedaży truskawek w sklepie pana Jana.
| Rodzaj opakowania | Masa truskawek w opakowaniu | Cena opakowania z truskawkami |
| duże | 1 kg | 18 zł |
| średnie | 0,5 kg | 10 zł |
| małe | 0,25 kg | 6 zł |
Oblicz, jaką kwotę otrzymał pan Jan ze sprzedaży wszystkich truskawek.
Z trzech jednakowych klocków w kształcie sześcianu i jednego klocka w kształcie ostrosłupa prawidłowego czworokątnego zbudowano dwie wieże (zobacz rysunek).
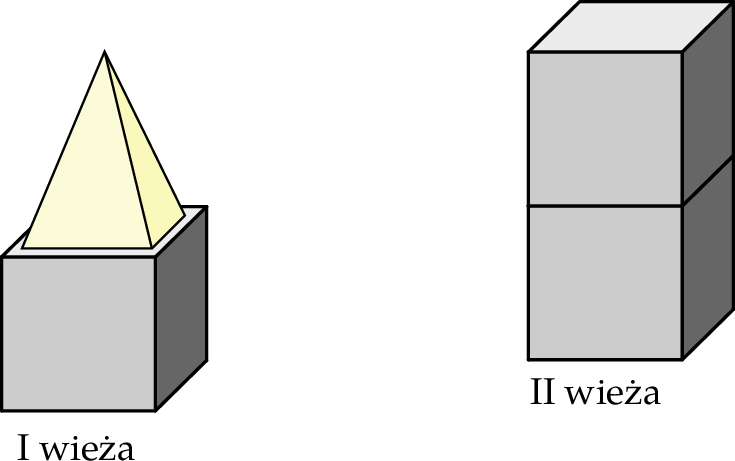
Krawędź sześcianu ma długość 10 cm. Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 9 cm, a jego objętość jest równa 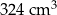 . Oblicz różnicę wysokości obu wież.
. Oblicz różnicę wysokości obu wież.

