/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2025/Materiały pomocnicze
Przykładowe zadania
z Matematyki Egzamin ósmoklasisty 2025
informator CKE
Zadania zamknięte
Kasia zauważyła, że ścienny zegar w mieszkaniu babci w ciągu każdej godziny spóźnia się o kolejne 4 minuty. Gdy poprawnie działający zegarek Kasi wskazywał godzinę 9:00, dziewczynka ustawiła na zegarze ściennym tę samą godzinę. Przyjęła, że w każdym kolejnym kwadransie opóźnienie jest jednakowe. Którą godzinę wskaże – zgodnie z założeniami Kasi – zegar ścienny po upływie 2 godzin i 3 kwadransów od godziny 9:00, jeżeli zachowana zostanie zaobserwowana tendencja opóźniania?
A) 11:34 B) 11:37 C) 11:41 D) 11:56
Marta zapisała w systemie rzymskim cztery liczby: CLXX, CXC, CCLXX oraz CCL. Która z nich znajduje się na osi liczbowej najbliżej liczby 200?
A) CLXX B) CXC C) CCLXX D) CCL
Do trzech jednakowych naczyń wlano tyle wody, że w pierwszym naczyniu woda zajmowała  pojemności, w drugim:
pojemności, w drugim:  pojemności, a w trzecim:
pojemności, a w trzecim:  pojemności danego naczynia.
pojemności danego naczynia.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W drugim naczyniu było mniej wody niż w trzecim naczyniu. | P | F |
| W pierwszym i drugim naczyniu łącznie było tyle samo wody, co w trzecim naczyniu. | P | F |
W każdej z dwóch torebek znajdują się 32 cukierki: 17 pomarańczowych, 10 jabłkowych i 5 truskawkowych. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Do pierwszej torebki należy dołożyć A/B cukierki truskawkowe, aby wszystkie znajdujące się w niej cukierki truskawkowe stanowiły 25% liczby wszystkich cukierków w tej torebce.
A) 3 B) 4
Liczba cukierków pomarańczowych, które należy wyjąć z drugiej torebki, aby wśród pozostałych w niej cukierków było 40% pomarańczowych, jest C/D niż 5.
C) mniejsza D) większa
Za 30 dag orzechów pistacjowych zapłacono 15,75 zł.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Za 40 dag tych orzechów należy zapłacić 21 zł. | P | F |
| Cena 1 kg tych orzechów jest równa 52,50 zł. | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 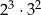 jest równa A/B .
jest równa A/B .
A) 36 B) 72
Wartość wyrażenia 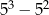 jest równa C/D .
jest równa C/D .
C) 5 D) 100
Wojtek narysował cztery figury (I–IV) składające się z kwadratów i trójkątów równobocznych (zobacz rysunek). Zamierza on dorysować do każdej figury jeden kwadrat albo jeden trójkąt, aby otrzymać z nich siatki graniastosłupa.
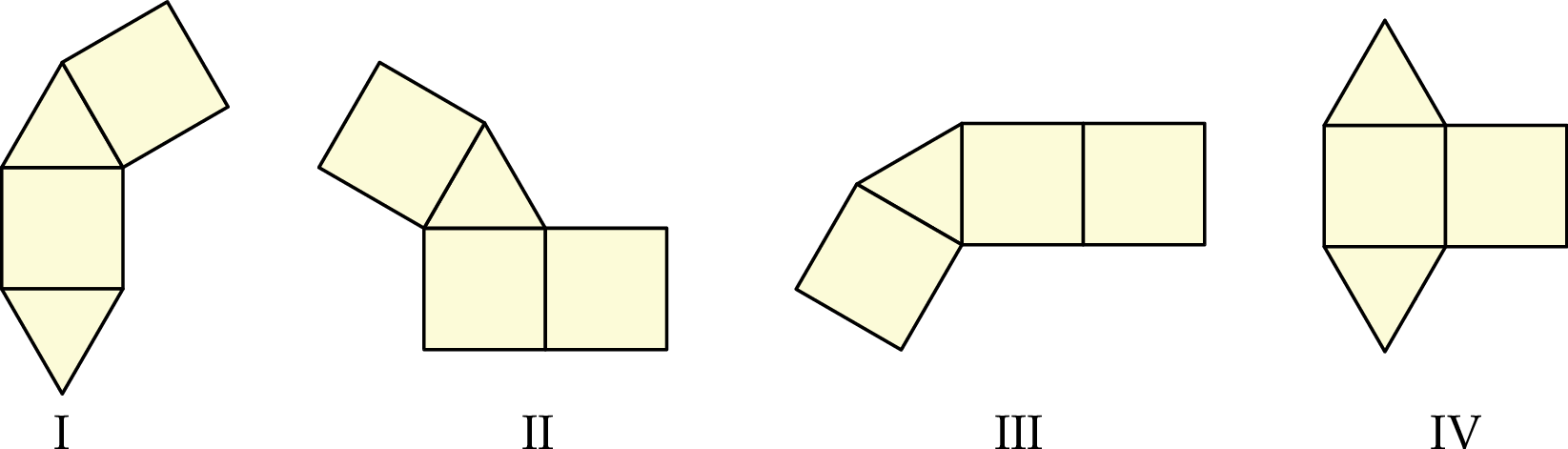
Z której figury nie da się w sposób zaplanowany przez Wojtka otrzymać siatki graniastosłupa?
A) I B) II C) III D) IV
Rzucamy raz symetryczną sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że w rzucie tą kostką wypadnie liczba oczek większa od 2, ale mniejsza od 6?
A)  B)
B)  C)
C)  D)
D) 
Dane jest wyrażenie
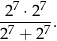
Czy wartość tego wyrażenia jest liczbą podzielną przez 8? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | każdy z wykładników jest liczbą nieparzystą. |
| B) | wykładnik potęgi 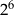 nie jest podzielny przez 8. nie jest podzielny przez 8. |
| C) | wartość tego wyrażenia można zapisać w postaci 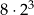 . . |
Witek ma trzy jednakowe prostopadłościenne klocki. W każdym z tych klocków dwie ściany są kwadratami, a cztery pozostałe – prostokątami. Z tych klocków zbudował figurę przedstawioną na rysunku.
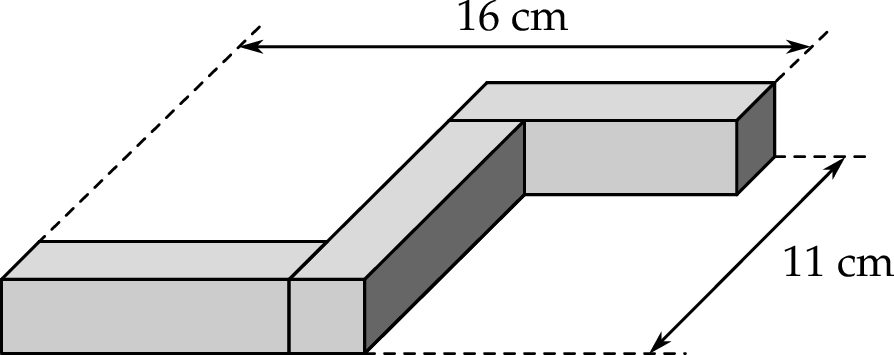
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dłuższe krawędzie prostopadłościennego klocka mają po 8 cm. | P | F |
Objętość jednego klocka jest równa 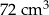 . . | P | F |
Napój otrzymano, po tym jak rozcieńczono 450 ml soku wodą w stosunku 1 : 10. Ile napoju otrzymano?
A) Więcej niż 4 litry, ale mniej niż 4,5 litra.
B) Dokładnie 4,5 litra.
C) Więcej niż 4,5 litra, ale mniej niż 5 litrów.
D) Dokładnie 5 litrów.
E) Więcej niż 5 litrów.
Dane są trzy wyrażenia:
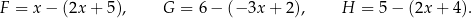
Dla każdej wartości  prawdziwa jest równość
prawdziwa jest równość
A) 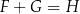 B)
B) 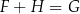 C)
C) 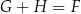 D)
D) 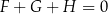
Zapisano sumę szesnastu jednakowych składników:
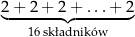
Wartość tej sumy jest równa
A) 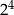 B)
B) 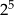 C)
C) 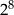 D)
D) 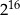
Informacja do zadań 14 i 15
Mateusz mieszka w odległości 4 km od szkoły. Część drogi do szkoły pokonuje pieszo, idąc do przystanku autobusowego. Tam czeka na autobus, a następnie wsiada do niego i jedzie do szkoły. Pewnego dnia, gdy był już na przystanku, stwierdził, że zapomniał zabrać zeszyt, więc wrócił po niego do domu. Wykres przedstawia, jak tego dnia zmieniała się odległość Mateusza od domu w zależności od czasu.
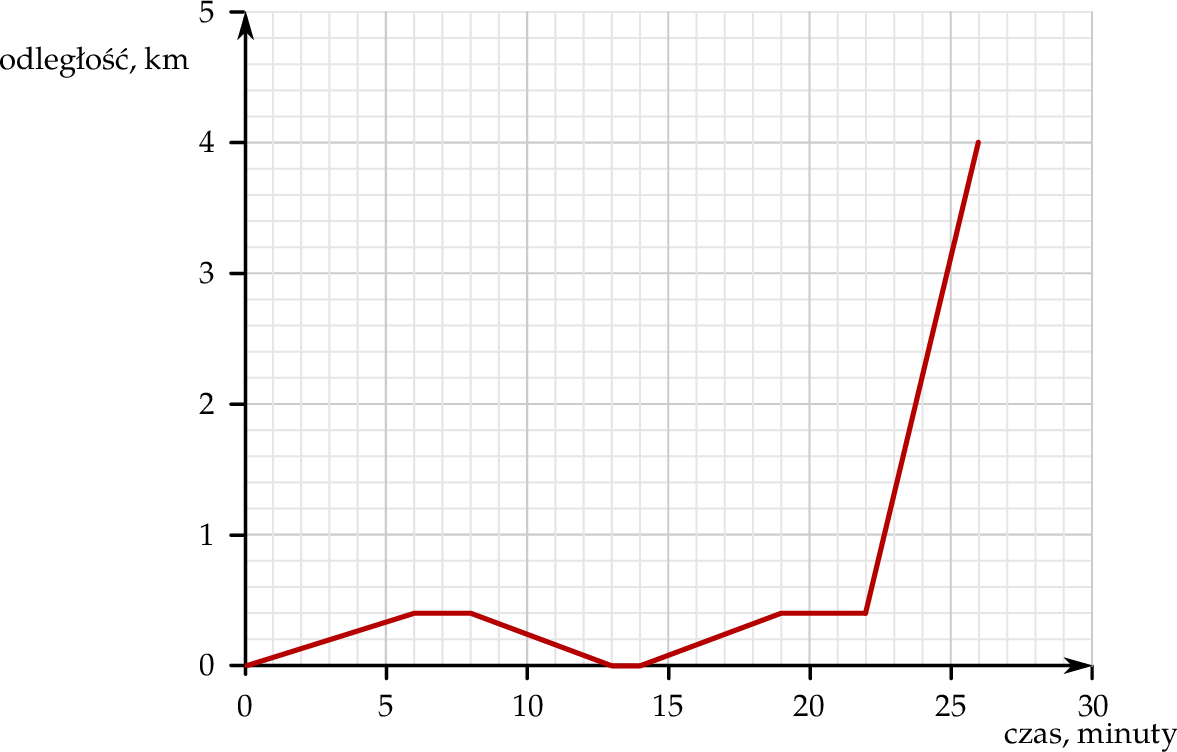
Od momentu, gdy Mateusz zawrócił z przystanku do domu, do momentu, gdy dotarł ponownie na przystanek, upłynęło
A) 11 minut. B) 13 minut. C) 14 minut. D) 16 minut.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dom Mateusza znajduje się w odległości 400 m od przystanku autobusowego. | P | F |
Autobus drogę między przystankami pokonał z prędkością 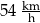 . . | P | F |
Dane są cztery liczby: 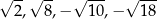 . Suma trzech spośród nich jest równa 0. Którą liczbę należy odrzucić, aby suma pozostałych trzech liczb była równa 0?
. Suma trzech spośród nich jest równa 0. Którą liczbę należy odrzucić, aby suma pozostałych trzech liczb była równa 0?
A) 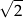 B)
B) 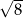 C)
C) 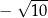 D)
D) 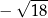
Na rysunku przedstawiono prostopadłościenny klocek o wymiarach 8 cm, 7 cm i 3 cm oraz sposób, w jaki rozcięto go na cztery części: sześcian (I) i trzy prostopadłościany (II, III, IV).
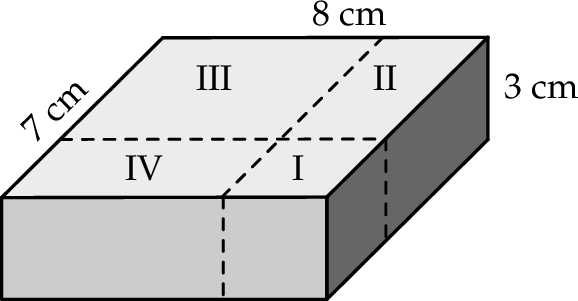
Objętość prostopadłościanu II jest równa
A) 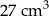 B)
B) 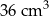 C)
C) 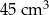 D)
D) 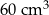
Na spektakl dostępne były bilety normalne w jednakowej cenie oraz bilety ulgowe, z których każdy kosztował o 50% mniej niż normalny. Pani Anna za 3 bilety normalne i 2 bilety ulgowe zapłaciła 120 złotych. Na ten sam spektakl pan Jacek kupił 2 bilety normalne i 3 ulgowe, a pan Marek kupił 2 bilety normalne i 1 ulgowy. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Pan Jacek zapłacił za bilety A/B .
A) 120 zł B) 105 zł
Pani Anna zapłaciła za bilety o C/D więcej niż pan Marek.
C) 45 zł D) 30 zł
Na diagramie przedstawiono wielkość produkcji krzeseł w firmie Mebelix w 2015 r. i 2016 r.
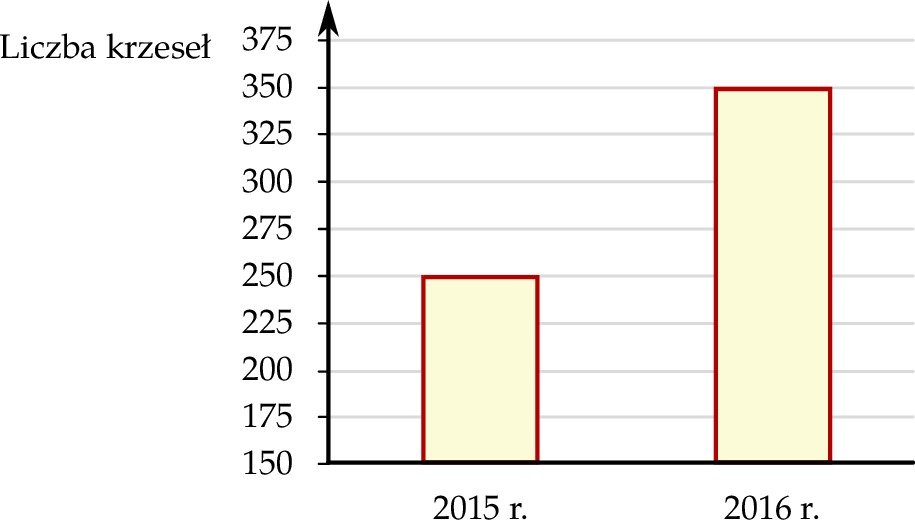
Czy liczba wyprodukowanych krzeseł w roku 2016 była o 100% większa od liczby wyprodukowanych krzeseł w roku 2015? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | drugi słupek na wykresie jest 2 razy wyższy od pierwszego. |
| B) | liczba krzeseł wyprodukowanych w 2016 roku jest o 40% większa niż liczba krzeseł wyprodukowanych w 2015 roku. |
| C) | w roku 2016 wyprodukowano o 250 krzeseł więcej niż w roku 2015. |
Na rysunku przedstawiono kwadraty 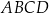 ,
, 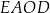 i
i 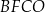 . Punkt
. Punkt 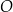 jest punktem przecięcia przekątnych kwadratu
jest punktem przecięcia przekątnych kwadratu 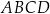 .
.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole kwadratu 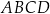 jest równe sumie pól kwadratów jest równe sumie pól kwadratów 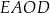 i i 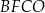 . . | P | F |
Obwód kwadratu 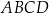 jest równy sumie długości wszystkich przekątnych kwadratów jest równy sumie długości wszystkich przekątnych kwadratów 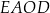 i i 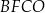 . . | P | F |
Drewnianą kostkę sześcienną o krawędzi długości 30 cm rozcięto na 27 jednakowych mniejszych sześciennych kostek. Z ośmiu takich małych kostek ułożono nowy sześcian.
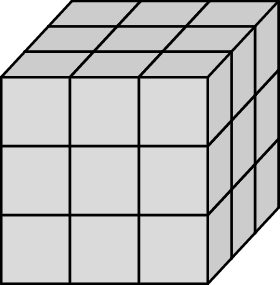
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole powierzchni nowego sześcianu jest równe 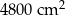 . . | P | F |
Objętość nowego sześcianu jest równa 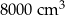 . . | P | F |
Na okręgu o środku w punkcie 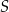 zaznaczono punkty
zaznaczono punkty 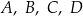 , a następnie narysowano odcinki
, a następnie narysowano odcinki 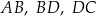 oraz
oraz 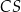 (zobacz rysunek).
(zobacz rysunek).

Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Trójkąt 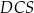 A/B równoramienny.
A/B równoramienny.
A) jest B) nie jest
Długość odcinka 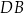 jest równa C/D .
jest równa C/D .
C) sumie długości odcinków 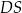 i
i 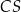 D) długości odcinka
D) długości odcinka 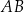
Zadania otwarte
Uzasadnij, że pierwszy dzień września i pierwszy dzień grudnia tego samego roku wypadają w tym samym dniu tygodnia.
W tabeli podano wybrane informacje na temat dwóch rodzajów herbat, które pije rodzina Nowaków.
| Rodzaj opakowania | Zawartość opakowania | Cena opakowania | Ilość herbaty potrzebna do zaparzenia jednego kubka naparu |
| herbata w torebkach | 50 torebek | 8,50 zł | 1 torebka |
| herbata sypka | 50 g | 5,00 zł | 2 g |
Rodzina ta wypija dziennie średnio 12 kubków herbaty i zamierza kupić możliwie najmniejszą liczbę opakowań herbaty jednego rodzaju, aby wystarczyło jej na 30 dni. Oblicz koszt zakupu herbaty w torebkach oraz koszt zakupu herbaty sypkiej.
W układzie współrzędnych na płaszczyźnie dane są punkty: 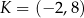 i
i 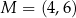 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 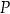 takiego, że jeden z trzech punktów
takiego, że jeden z trzech punktów 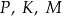 jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
W tabeli przedstawiono ceny kupna i sprzedaży dwóch walut w kantorze Pik.
| Kupno | Sprzedaż | |
| 1 dolar | 4,18 zł | 4,25 zł |
| 1 funt brytyjski | 5,10 zł | 5,22 zł |
Marcin chce wymienić 400 funtów brytyjskich na dolary. W tym celu musi najpierw wymienić funty na złotówki, a następnie – otrzymane złotówki na dolary. Oblicz, ile dolarów otrzyma Marcin, jeżeli wymieni walutę w kantorze Pik.
Bok 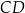 kwadratu
kwadratu 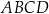 podzielono punktami
podzielono punktami 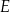 i
i 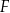 na trzy odcinki równej długości. Przez wierzchołek
na trzy odcinki równej długości. Przez wierzchołek 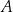 kwadratu i przez punkt
kwadratu i przez punkt 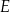 poprowadzono prostą (zobacz rysunek). Pole trójkąta
poprowadzono prostą (zobacz rysunek). Pole trójkąta 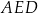 jest równe
jest równe 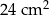 .
.
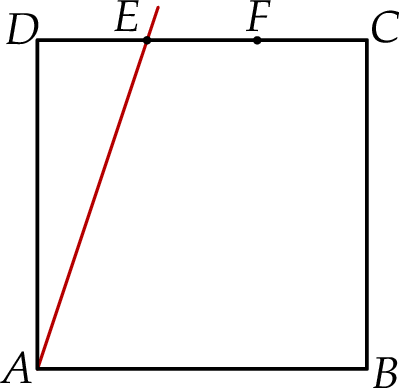
Oblicz pole kwadratu 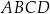 .
.
W pierwszym zbiorniku było cztery razy więcej litrów wody niż w drugim. Do każdego zbiornika wlano po 6 litrów wody. Teraz w pierwszym zbiorniku jest dwa razy więcej litrów wody niż w drugim zbiorniku. Oblicz, ile łącznie litrów wody jest w obu zbiornikach.
Prostokąt  podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe (zobacz rysunek).
podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe (zobacz rysunek).
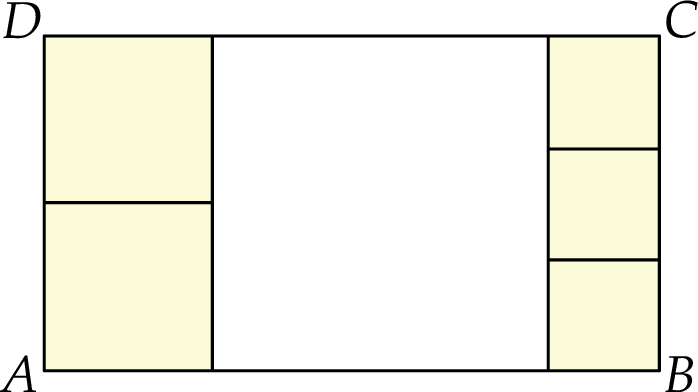
Uzasadnij, że pole dużego kwadratu jest większe niż połowa pola prostokąta  .
.
Prostokątny pasek papieru pocięto na cztery części w sposób przedstawiony na rysunku 1. Z tych części ułożono figurę w kształcie kwadratu tak, jak pokazano na rysunku 2. Pole tego kwadratu jest równe 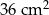 .
.
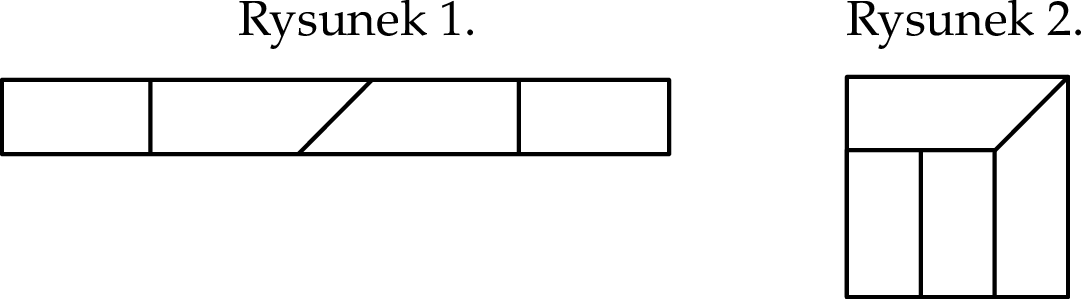
Oblicz obwód paska papieru przed pocięciem.
Trzy sąsiadki zamówiły wspólnie kawę w sklepie internetowym. Kawa dla pani Malinowskiej miała kosztować 120 zł, a dla pani Wiśniewskiej i dla pani Śliwińskiej – po 90 zł. Sąsiadki przy zakupie otrzymały rabat i za zamówioną kawę zapłaciły 260 zł. Oblicz, ile pieniędzy powinna zapłacić każda z pań, aby jej wpłata była proporcjonalna do pierwotnej wartości zamówienia.
Proste  i
i 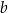 są równoległe. Półproste
są równoległe. Półproste 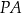 i
i 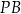 przecinają te proste, w punktach
przecinają te proste, w punktach 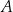 i
i 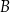 w wyniku czego tworzą z nimi kąty ostre o miarach podanych na rysunku.
w wyniku czego tworzą z nimi kąty ostre o miarach podanych na rysunku.
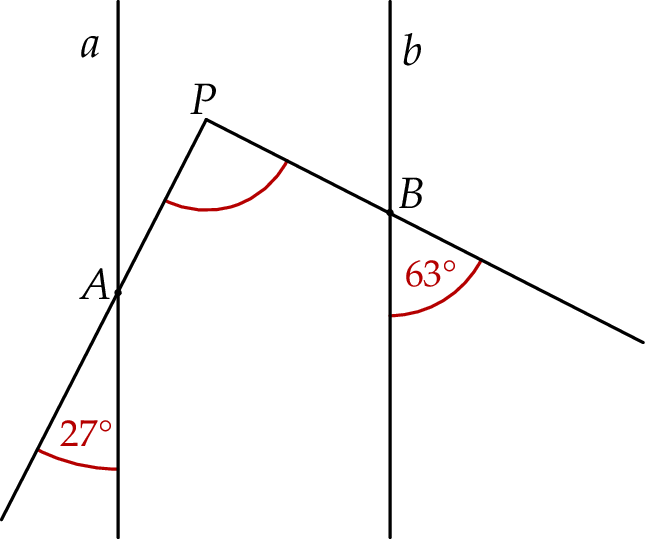
Uzasadnij, że kąt 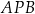 jest prosty.
jest prosty.
Trójkąt przedstawiony na rysunku jest ścianą boczną ostrosłupa prawidłowego czworokątnego.

Oblicz pole powierzchni całkowitej ostrosłupa o takich wymiarach.
Jaskinię Książęcą może zwiedzić codziennie tylko dziesięć grup, które wchodzą po jednej w jednakowych odstępach czasu. Pierwsza grupa rozpoczyna zwiedzanie o 9:00, a ostatnia – o 16:30. Grupa harcerzy przyszła zwiedzić jaskinię o godzinie 13:25. Oblicz, ile co najmniej minut harcerze będą czekali na wejście do jaskini.
Agnieszka zapisała liczbę czterocyfrową podzielną przez 7. Skreśliła w tej liczbie cyfrę jedności i otrzymała liczbę 496. Jaką liczbę czterocyfrową zapisała Agnieszka?
Prostokąt o bokach długości 12 i 6 podzielono na dwa prostokąty (zobacz rysunek). Obwód jednego z prostokątów otrzymanych w wyniku podziału jest 2 razy większy od obwodu drugiego prostokąta.

Oblicz wymiary prostokąta o mniejszym obwodzie.
Na okręgu o środku 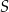 i promieniu
i promieniu 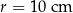 zaznaczono punkty
zaznaczono punkty 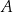 i
i 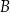 , takie że odcinek
, takie że odcinek 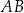 ma długość 16 cm. Następnie dorysowano odcinki
ma długość 16 cm. Następnie dorysowano odcinki 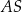 i
i 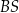 .
.
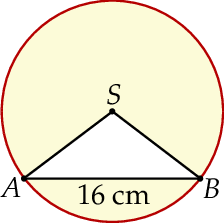
Oblicz pole zacieniowanej figury. W obliczeniach przyjmij 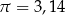 .
.

