/Szkoła podstawowa/Zadania testowe/Prawdopodobieństwo

Zadanie nr 1403786

Dodaj do ulubionych
Dodaj do rozwiązanych

W pudełku są tylko kule białe i czarne, przy czym kul czarnych jest o 5 więcej niż kul białych, a prawdopodobieństwo wylosowania kuli białej jest dwa razy mniejsze, niż prawdopodobieństwo wylosowania kuli czarnej. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

W pudełku jest więcej niż 12 kul. PF
Po dołożeniu do pudełka 3 kul czarnych, prawdopodobieństwo wylosowania kuli białej będzie 3 razy mniejsze niż prawdopodobieństwo wylosowania kuli czarnej. PF

Rozwiązanie

Sposób I

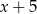Jeżeli kul białych jest x , to kul czarnych jest x + 5 i z podanej informacji o prawdopodobieństwach mamy

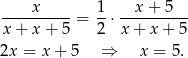
----x-----= 1-⋅--x-+-5--- x + x + 5 2 x + x + 5 2x = x+ 5 ⇒ x = 5 .

W takim razie w pudełku jest 5 kul białych i 10 kul czarnych.

Jeżeli do pudełka dołożymy 3 kule czarne, to prawdopodobieństwa wylosowania kuli białej i czarnej będą odpowiednio równe

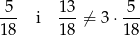
5 1 3 5 --- i --- ⁄= 3 ⋅--- 1 8 1 8 18

Sposób II

Jeżeli prawdopodobieństwo wylosowania kuli czarnej jest dwa razy większe niż kuli białej, to kul czarnych musi być dwa razy więcej niż kul białych. Z drugiej strony wiemy, że jest ich o 5 więcej, co oznacza, że kul białych i czarnych musi być odpowiednio 5 i 10.

Jeżeli prawdopodobieństwo wylosowania kuli białej ma być 3 razy mniejsze niż prawdopodobieństwo wylosowania kuli czarnej, to kul czarnych musi być 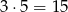3 ⋅5 = 15 , więc trzeba dołożyć 5 kul czarnych.  
Odpowiedź: P, F

Wersja PDF