Oblicz stosunek objętości kuli wpisanej w czworościan foremny do objętości kuli opisanej na tym czworościanie.
Zróbmy rysunek.
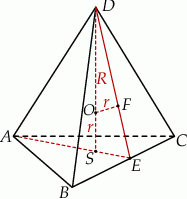
Środek kuli opisanej na czworościanie to punkt, który jest jednakowo odległy, powiedzmy o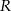 
, od wszystkich wierzchołków. Podobnie, środek kuli wpisanej jest jednakowo odległy, powiedzmy o 
, od wszystkich ścian. W przypadku czworościanu foremnego punkty te pokrywają się (jest to też punkt przecięcia się wysokości). To co mamy obliczyć, to iloraz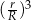 
.
Korzystamy z podobieństwa trójkątów prostokątnych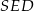 
i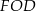 
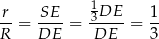
Stąd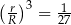 
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
