Zadanie nr 6089323
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 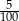 C)
C) 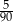 D)
D) 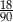
Rozwiązanie
Wszystkich liczb dwucyfrowych jest
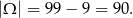
Sposób I
Jest 18 liczb dwucyfrowych podzielnych przez 5:
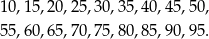
Interesujące nas prawdopodobieństwo jest więc równe
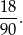
Sposób II
Jeżeli nie chcemy wypisywać wszystkich liczb dwucyfrowych podzielnych przez 5, to możemy obliczyć ile ich jest. Cyfra jedności takiej liczby to 0 lub 5, a cyfrę dziesiątek możemy wybrać na 9 sposobów (nie może być zero). Jest więc
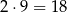
takich liczb. Interesujące nas prawdopodobieństwo jest więc równe
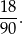
Odpowiedź: D

