/Szkoła średnia/Geometria/Geometria analityczna/Parabola

Zadanie nr 2873808

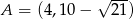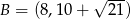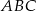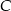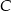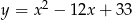Punkty √ --- A = (4,10 − 2 1) i √ --- B = (8,1 0+ 2 1) są wierzchołkami trójkąta prostokątnego ABC , o kącie prostym przy wierzchołku C . Oblicz współrzędne wierzchołka C tego trójkąta, wiedząc, że leży on na paraboli o równaniu y = x2 − 12x + 3 3 .

Wersja PDF

Rozwiązanie

Na początku naszkicujmy opisaną sytuację. Aby to zrobić zapiszmy podane równanie paraboli w postaci kanonicznej.

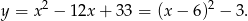
y = x 2 − 1 2x+ 33 = (x − 6)2 − 3.

Jest to więc parabola 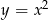y = x2 przesunięta o 6 jednostek w prawo i o 3 jednostki w dół. Robimy szkic.

PIC

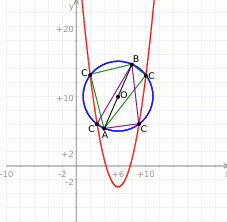
Oczywiście trudno jest wykonać dokładny rysunek, ale dokładny rysunek nie jest nam potrzebny – chcemy tylko ustalić o co chodzi.

Skoro trójkąt 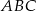ABC ma być prostokątny i 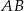AB ma być przeciwprostokątną, to punkt 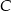C musi leżeć na okręgu o średnicy 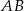AB . Widać więc co musimy zrobić: napiszemy równanie okręgu o średnicy 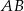AB i znajdziemy jego punkty wspólne z podaną parabolą.

Środek odcinka 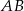AB ma współrzędne

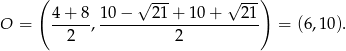
( √ --- √ ---) 4 + 8 10 − 21 + 10 + 21 O = ------,---------------------- = (6,10). 2 2

Aby napisać równanie okręgu potrzebujemy jeszcze promienia, czyli długości odcinka 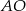AO .

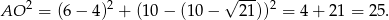
√ --- AO 2 = (6 − 4)2 + (10 − (10 − 21))2 = 4 + 21 = 25.

Zatem promień ma długość 5 i okrąg o średnicy 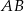AB ma równanie

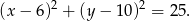
(x − 6)2 + (y− 10)2 = 25.

Pozostało rozwiązać układ równań

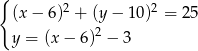
{ 2 2 (x − 6) + (y − 10) = 25 y = (x − 6 )2 − 3

Podstawiając 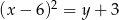(x− 6)2 = y + 3 z drugiego równania do pierwszego mamy

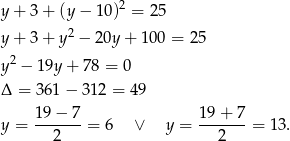
y + 3 + (y − 10)2 = 2 5 y + 3 + y2 − 20y + 10 0 = 25 2 y − 19y + 7 8 = 0 Δ = 361 − 312 = 49 y = 19-−-7-= 6 ∨ y = 19-+-7-= 13. 2 2

Stąd odpowiednio

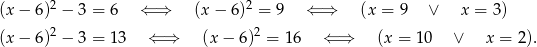
2 2 (x − 6) − 3 = 6 ⇐ ⇒ (x − 6) = 9 ⇐ ⇒ (x = 9 ∨ x = 3) (x − 6)2 − 3 = 1 3 ⇐ ⇒ (x − 6)2 = 16 ⇐ ⇒ (x = 10 ∨ x = 2).

Są zatem 4 takie punkty: 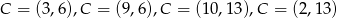C = (3,6),C = (9,6),C = (10,13),C = (2,13) .  
Odpowiedź: C = (3,6)∨ C = (9,6) ∨ C = (10,13) ∨ C = (2,13)

Wersja PDF