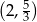/Szkoła średnia/Geometria/Geometria analityczna/Parabola

Zadanie nr 4168511

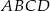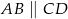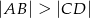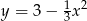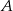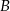Wszystkie wierzchołki trapezu ABCD (AB ∥ CD i |AB | > |CD | ) leżą na paraboli o równaniu y = 3− 13x2 . Wierzchołki A i B są punktami przecięcia tej paraboli z osią 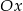Ox . Oblicz współrzędne wierzchołka trapezu o obu współrzędnych dodatnich, dla którego pole trapezu jest równe 25 3 .

Wersja PDF

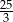Rozwiązanie

Dana parabola

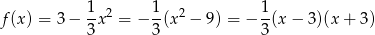
1 1 1 f (x) = 3 − --x2 = − -(x 2 − 9 ) = −-(x − 3)(x + 3 ) 3 3 3

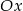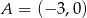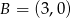przecina oś Ox w punktach A = (− 3,0) i B = (3,0) , a jej wierzchołek jest w punkcie

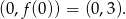
(0,f (0)) = (0,3).

Szkicujemy opisaną sytuację.

PIC

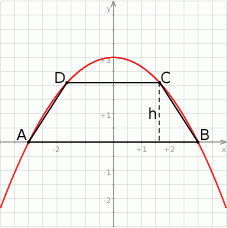
Jeżeli oznaczymy 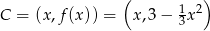( ) C = (x,f(x)) = x,3 − 13x 2 , to

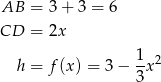
AB = 3+ 3 = 6 CD = 2x h = f(x) = 3 − 1-x2 3

i pole trapezu jest równe

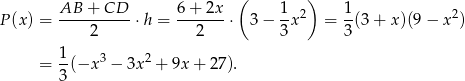
AB + CD 6 + 2x ( 1 ) 1 P (x) = ---------- ⋅h = -------⋅ 3 − --x2 = --(3+ x )(9− x2) 2 2 3 3 1- 3 2 = 3 (−x − 3x + 9x + 27).

Dziedziną tej funkcji jest przedział 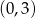(0 ,3) . Pozostało teraz rozwiązać równanie

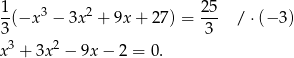
1(−x 3 − 3x 2 + 9x + 27) = 25 / ⋅(− 3) 3 3 x3 + 3x2 − 9x − 2 = 0 .

Szukamy teraz pierwiastków całkowitych tego równania – sprawdzamy dzielniki wyrazu wolnego. Jednym z pierwiastków jest 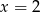x = 2 , więc dzielimy lewą stronę równania przez 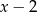x − 2 . My zrobimy to grupując wyrazy.

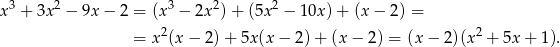
x3 + 3x2 − 9x − 2 = (x 3 − 2x2)+ (5x2 − 10x) + (x − 2) = 2 2 = x (x− 2)+ 5x(x − 2) + (x − 2) = (x − 2 )(x + 5x+ 1).

Rozkładamy jeszcze trójmian w nawiasie.

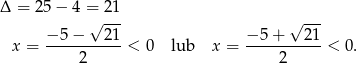
Δ = 25 − 4 = 21 √ --- √ --- x = −-5−----21-< 0 lub x = −-5-+---21-< 0. 2 2

Ponieważ z założenia 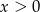x > 0 , mamy stąd 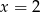x = 2 i

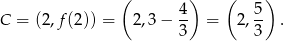
( ) ( ) C = (2,f (2)) = 2,3− 4- = 2, 5 . 3 3

 
Odpowiedź: ( ) 2, 5 3

Wersja PDF