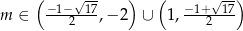Zadanie nr 4410026
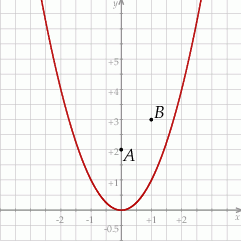
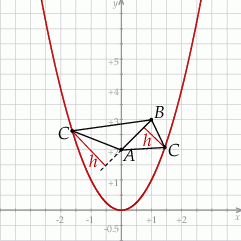
Dane są parabola o równaniu 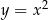 oraz punkty
oraz punkty 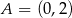 i
i 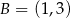 (zobacz rysunek).
(zobacz rysunek).
Rozpatrujemy wszystkie trójkąty 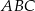 , których wierzchołek
, których wierzchołek 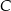 leży na tej paraboli. Niech
leży na tej paraboli. Niech 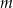 oznacza pierwszą współrzędną punktu
oznacza pierwszą współrzędną punktu 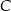 .
.
- Wyznacz pole
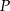 trójkąta
trójkąta 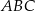 jako funkcję zmiennej
jako funkcję zmiennej 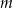 .
. - Wyznacz wszystkie wartości
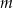 , dla których trójkąt
, dla których trójkąt 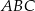 jest ostrokątny.
jest ostrokątny.
Rozwiązanie
- Niech
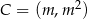 będzie dowolnym punktem danej paraboli. Pole trójkąta
będzie dowolnym punktem danej paraboli. Pole trójkąta 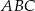 obliczymy na dwa sposoby.
obliczymy na dwa sposoby. Sposób I
Korzystamy ze wzoru na pole trójkąta o wierzchołkach
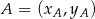 ,
, 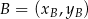 i
i 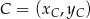 .
. 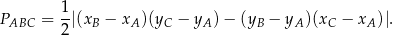
Mamy zatem
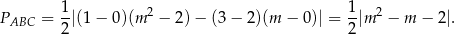
To jednak nie koniec, bo nie dla każdej wartości parametru
 punkty
punkty  ,
,  i
i 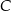 są wierzchołkami trójkąta. Tak jest tylko, gdy
są wierzchołkami trójkąta. Tak jest tylko, gdy 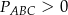 (czyli gdy punkt
(czyli gdy punkt 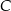 nie leży na prostej
nie leży na prostej 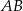 ). Sprawdźmy kiedy tak nie jest.
). Sprawdźmy kiedy tak nie jest. 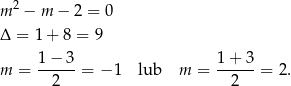
Sposób II
Tym razem skorzystamy ze wzoru na odległość punktu
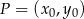 od prostej
od prostej 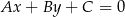 :
: 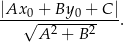
Wyznaczmy najpierw równanie prostej
 .
. 
Wiemy, że przechodzi ona przez punkt
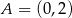 więc ma równanie postaci
więc ma równanie postaci 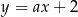 . Współczynnik
. Współczynnik  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 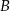 .
. 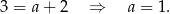
Prosta
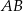 ma więc równanie
ma więc równanie 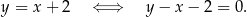
W takim razie wysokość
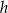 trójkąta
trójkąta 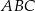 opuszczona na bok
opuszczona na bok 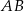 jest równa
jest równa 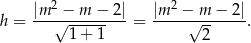
Pole trójkąta
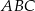 jest więc równe
jest więc równe 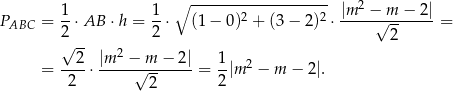
Dziedzinę otrzymanej funkcji wyznaczamy tak samo jak w poprzednim sposobie.
Odpowiedź: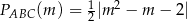 dla
dla 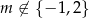
-
Sposób I
Jeżeli
 jest kątem trójkąta leżącym naprzeciw boku długości
jest kątem trójkąta leżącym naprzeciw boku długości  , to na mocy twierdzenia cosinusów
, to na mocy twierdzenia cosinusów 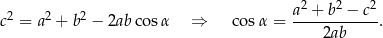
To oznacza, że
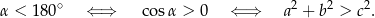
W takim razie trójkąt jest ostrokątny wtedy i tylko wtedy, gdy suma kwadratów dwóch krótszych boków jest większa od kwadratu najdłuższego boku. W naszej sytuacji mamy
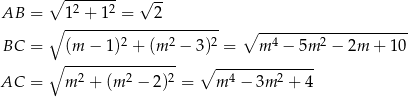
Niestety nie wiemy, który z tych odcinków jest najdłuższy, więc musimy rozwiązać trzy nierówności (wszystkie trzy muszą być jednocześnie spełnione).
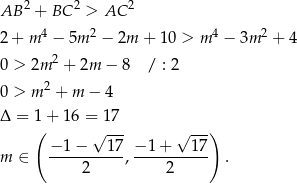
Kolejna nierówność to
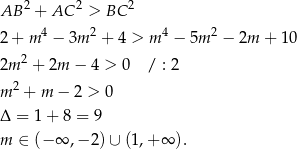
Część wspólna obu otrzymanych nierówności to
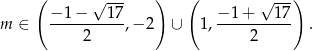
To jednak nie koniec, bo musimy się jeszcze zająć ostatnią z nierówności
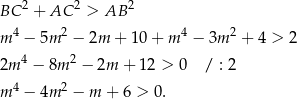
Sytuacja nie wygląda na specjalnie prostą, ale jeżeli zapiszemy lewą stronę w postaci
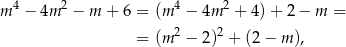
to widać, że wyrażenie to na pewno jest dodatnie dla
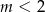 . Z drugiej strony wiemy już, że
. Z drugiej strony wiemy już, że 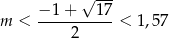
więc trzecia z nierówności jest zawsze spełniona.
Sposób II
Tym razem spróbujemy na popatrzeć na całą sytuację bardziej geometrycznie.
Po pierwsze zastanówmy się, czy jest możliwe, żeby kąt rozwarty trójkąta
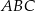 był kątem przy wierzchołku
był kątem przy wierzchołku 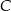 ? Aby tak było punkt
? Aby tak było punkt 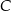 musiałby się znajdować wewnątrz koła o średnicy
musiałby się znajdować wewnątrz koła o średnicy 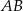 (dla punktów
(dla punktów 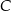 tego koła mamy
tego koła mamy 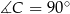 ). Jest to koło o środku
). Jest to koło o środku 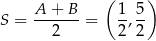
i promieniu
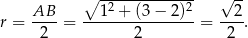
Koło to jest więc opisane nierównością
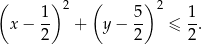
Sprawdźmy teraz, czy wewnątrz tego koła znajduje się jakikolwiek punkt
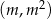 danej paraboli
danej paraboli 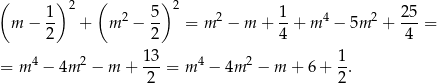
Zauważmy teraz, że jeżeli
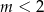 , to
, to 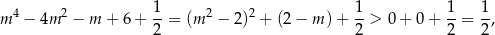
a jeżeli
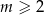 , to
, to 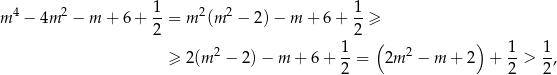
bo wyróżnik trójmianu w ostatnim nawiasie jest ujemny.
Udowodniliśmy więc, że koło o średnicy
 i dana parabola nie mają punktów wspólnych, czyli kąt rozwarty trójkąta
i dana parabola nie mają punktów wspólnych, czyli kąt rozwarty trójkąta  nie może się znajdować przy wierzchołku
nie może się znajdować przy wierzchołku 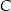 . W takim razie musimy tylko zagwarantować, aby kąty przy wierzchołkach
. W takim razie musimy tylko zagwarantować, aby kąty przy wierzchołkach 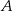 i
i 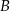 były ostre, a tak będzie, gdy punkt
były ostre, a tak będzie, gdy punkt 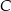 znajdzie się w pasie pomiędzy dwoma prostymi prostopadłymi do odcinka
znajdzie się w pasie pomiędzy dwoma prostymi prostopadłymi do odcinka 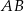 i przechodzącymi przez punkty
i przechodzącymi przez punkty 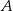 i
i 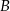 . Łatwo zauważyć, ze punkty
. Łatwo zauważyć, ze punkty 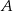 i
i 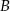 leżą na prostej
leżą na prostej 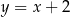 , więc proste prostopadłe do prostej
, więc proste prostopadłe do prostej 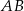 mają równania postaci
mają równania postaci 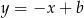 . Jeżeli podstawiamy współrzędne punktów
. Jeżeli podstawiamy współrzędne punktów 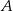 i
i 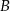 , to okaże się, że interesują nas proste
, to okaże się, że interesują nas proste 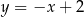 i
i 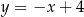 . Wyznaczamy teraz punkty wspólne tych prostych z daną parabolą. Najpierw pierwsza prosta
. Wyznaczamy teraz punkty wspólne tych prostych z daną parabolą. Najpierw pierwsza prosta 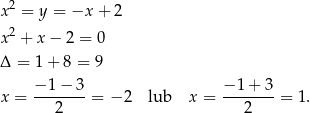
Otrzymujemy więc punkty
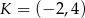 i
i 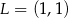 . Teraz druga z prostych
. Teraz druga z prostych 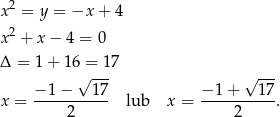
Drugich współrzędnych punktów
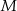 i
i 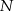 możemy nie obliczać, bo nie będą nam potrzebne. Jak ustaliliśmy wierzchołek
możemy nie obliczać, bo nie będą nam potrzebne. Jak ustaliliśmy wierzchołek 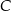 musi na paraboli znajdować się pomiędzy punktami
musi na paraboli znajdować się pomiędzy punktami 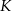 i
i 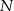 lub pomiędzy punktami
lub pomiędzy punktami 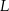 i
i 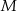 . Mamy w takim razie
. Mamy w takim razie 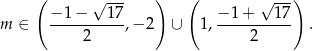
Odpowiedź: