/Szkoła średnia/Geometria/Geometria analityczna/Parabola

Zadanie nr 5305713

Dana jest parabola o równaniu 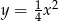1 2 y = 4x i punkt 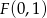F (0,1) . Wykaż, że każdy punkt leżący na paraboli jest równo oddalony od punktu 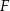F i prostej 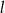l o równaniu y = − 1 .

Wersja PDF

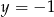Rozwiązanie

Po pierwsze naszkicujmy sobie tę parabolę.

PIC

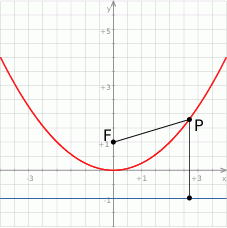
Jeżeli punkt 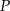P jest punktem podanej paraboli, to jest postaci 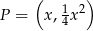( ) P = x, 14x2 . Jego odległość od prostej 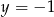y = − 1 jest równa 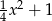1 2 4x + 1 . Obliczamy teraz długość odcinka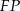 FP

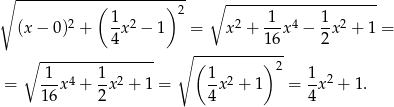
∘ -----------(---------)-- ∘ --------------------- 2 1- 2 2 2 -1- 4 1- 2 (x − 0) + 4 x − 1 = x + 16 x − 2x + 1 = ∘ ---------------- ∘ ------------- 1 1 (1 ) 2 1 = --x4 + --x2 + 1 = --x2 + 1 = -x 2 + 1 . 16 2 4 4

Gdyby ktoś nie zauważył, że wyrażenie pod pierwiastkiem to pełen kwadrat to można po prostu porównać ten pierwiastek z tym co mam wyjść, czyli z 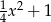1 x2 + 1 4 i przekształcać aż będzie 0=0.

Dla ciekawskich, każda parabola to zbiór punktów, które są równoodległe od pewnej prostej (zwanej kierownicą) i punktu (zwanego ogniskiem). W tym przykładzie kierownicą jest prosta 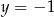y = − 1 , a ogniskiem podany punkt 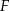F – dlatego zresztą się nazywa 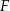F , od ’focal point’.

Wersja PDF