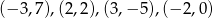/Szkoła średnia/Geometria/Geometria analityczna/Parabola

Zadanie nr 6766874

Punkty przecięcia paraboli 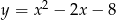2 y = x − 2x − 8 z prostą 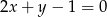2x + y − 1 = 0 są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.

Wersja PDF

Rozwiązanie

PIC

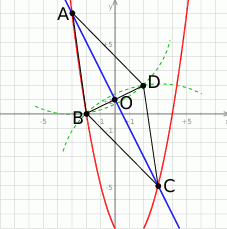
Na początku znajdźmy punkty wspólne podanej paraboli i prostej (porównujemy 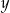y -ki).

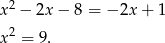
x2 − 2x− 8 = − 2x + 1 2 x = 9.

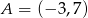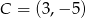Zatem punkty przecięcia to A = (− 3,7) i C = (3,− 5) . Dalszy plan działania jest następujący, mając końce przekątnej możemy wyliczyć jej długość. Potem, z podanego pola wyliczymy długość drugiej przekątnej. Mając długości przekątnych można wyliczyć długość boku i na koniec znajdziemy współrzędne pozostałych dwóch wierzchołków.

Liczymy

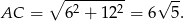
∘ --------- √ -- AC = 62 + 12 2 = 6 5.

Korzystając ze wzoru na pole z długościami przekątnych 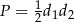1 P = 2d 1d2 , mamy

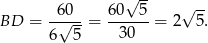
√ -- -60-- 6-0--5 √ -- BD = 6√ 5-= 30 = 2 5.

Ponieważ przekątne rombu dzielą się na połowy i są prostopadłe, z trójkąta prostokątnego 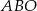ABO możemy wyliczyć długość boku rombu.

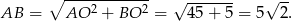
∘ ---2------2- √ ------- √ -- AB = AO + BO = 45+ 5 = 5 2.

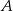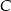Szukamy teraz punktów wspólnych okręgów o środkach w punktach A i C i promieniu 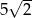√ -- 5 2 – innymi słowy szukamy 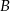B i D .

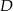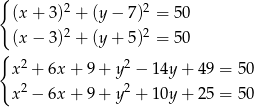
{ (x + 3)2 + (y − 7)2 = 5 0 (x − 3)2 + (y + 5)2 = 5 0 { x 2 + 6x + 9 + y 2 − 1 4y+ 49 = 50 2 2 x − 6x + 9 + y + 1 0y+ 25 = 50

Odejmując równania stronami (żeby skrócić kwadraty) mamy

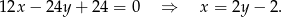
12x − 24y + 24 = 0 ⇒ x = 2y − 2.

Wstawiamy to do drugiego równania

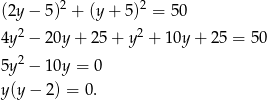
2 2 (2y − 5) + (y+ 5) = 50 4y2 − 20y + 25 + y2 + 10y + 2 5 = 50 2 5y − 10y = 0 y(y − 2) = 0.

Stąd 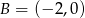B = (−2 ,0) i D = (2,2) .  
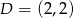Odpowiedź: (− 3,7),(2,2),(3,− 5),(− 2,0 )

Wersja PDF