/Szkoła średnia/Geometria/Geometria analityczna/Parabola

Zadanie nr 8122253

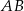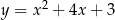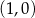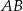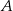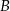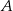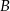Rozważmy cięciwy AB paraboli 2 y = x + 4x + 3 przechodzące przez punkt (1,0) , przy czym przez cięciwę AB rozumiemy prostą przecinającą tę parabolę w dwóch punktach A i B . Wyznacz współrzędne punktów A i B , dla których suma współrzędnych środka odcinka 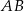AB cięciwy 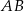AB jest równa − 2 .

Wersja PDF

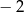Rozwiązanie

Parabola 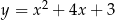2 y = x + 4x + 3 ma wierzchołek w punkcie

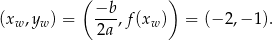
( −b ) (xw ,yw) = ----,f(xw) = (− 2,− 1). 2a

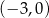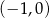Można też wyliczyć miejsca zerowe paraboli, są to punkty (− 3,0) i (− 1,0) . Teraz możemy naszkicować o co chodzi.

PIC

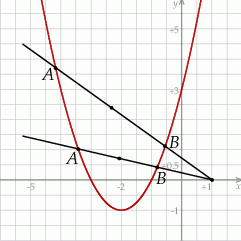
Proste przechodzące przez punkt 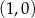(1,0) możemy zapisać w postaci 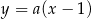y = a(x− 1) , gdzie 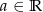a ∈ R (tak naprawdę pomijamy pionową prostą przechodzącą przez 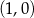(1,0) , która nie jest tej postaci, jednak ona przecina parabolę tylko w jednym punkcie). Punkty wspólne tej prostej i danej paraboli wyznaczamy z równania

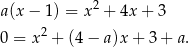
2 a(x − 1) = x + 4x + 3 0 = x 2 + (4 − a)x + 3 + a.

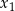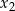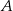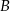Tak naprawdę nie interesują nas rozwiązania x 1 i x 2 tego równania (czyli punkty A i B ), ale wyrażenie 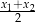x1+x2 2 , które jest równe pierwszej współrzędnej środka 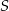S odcinka 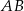AB . Na mocy wzorów Viète’a mamy

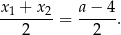
x + x a− 4 -1----2-= -----. 2 2

Wyliczmy teraz drugą współrzędną punktu 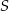S

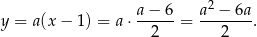
a − 6 a2 − 6a y = a(x− 1) = a ⋅------= -------. 2 2

Zatem 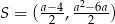a−-4-a2−6a S = ( 2 , 2 ) .

Korzystamy teraz z podanej informacji o sumie współrzędnych punktu 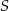S .

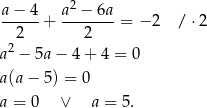
a− 4 a2 − 6a ------+ --------= − 2 / ⋅2 2 2 a2 − 5a− 4+ 4 = 0 a(a− 5) = 0 a = 0 ∨ a = 5 .

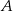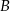Pozostało zobaczyć jakie są współrzędne punktów A i B dla tych wartości a . Mamy odpowiednio równania

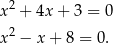
x2 + 4x + 3 = 0 2 x − x + 8 = 0.

Drugie równanie nie ma rozwiązań, obliczmy pierwiastki pierwszego.

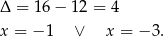
Δ = 1 6− 1 2 = 4 x = − 1 ∨ x = − 3.

Zatem szukane końce cięciwy to 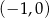(− 1,0) i (− 3,0) .  
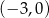Odpowiedź: 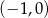(− 1,0) i (− 3,0)

Wersja PDF