Zadanie nr 4947738
Liczba pięciocyfrowa  jest podzielna przez 3, ale nie jest podzielna przez 6. Trzy początkowe cyfry tej liczby to: 4, 1, 3, a dwie pozostałe cyfry są większe od 4. Ile może być równe
jest podzielna przez 3, ale nie jest podzielna przez 6. Trzy początkowe cyfry tej liczby to: 4, 1, 3, a dwie pozostałe cyfry są większe od 4. Ile może być równe  ? Podaj wszystkie możliwości.
? Podaj wszystkie możliwości.
Rozwiązanie
Szukamy liczby postaci 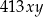 . Ponadto liczba ta musi być nieparzysta (bo inaczej dzieliłaby się przez 6), więc
. Ponadto liczba ta musi być nieparzysta (bo inaczej dzieliłaby się przez 6), więc 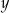 musi być nieparzyste.
musi być nieparzyste.
Sposób I
Liczba ta ma być podzielna przez 3, więc suma jej cyfr musi być podzielna przez 3. Ponieważ 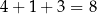 , suma cyfr otrzymanej liczby musi być równa 18, 21 lub 24 (bo
, suma cyfr otrzymanej liczby musi być równa 18, 21 lub 24 (bo  i
i 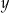 mogą być równe: 5, 6, 7, 8, 9).
mogą być równe: 5, 6, 7, 8, 9).
Jeżeli suma cyfr jest równa 18 to mamy 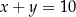 , czyli musi być
, czyli musi być 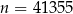 .
.
Jeżeli suma cyfr jest równa 21 to mamy 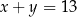 , czyli
, czyli 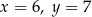 lub
lub 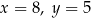 (bo
(bo 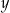 musi być nieparzyste). Mamy więc w tym przypadku dwie liczby:
musi być nieparzyste). Mamy więc w tym przypadku dwie liczby: 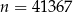 lub
lub 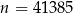 .
.
Jeżeli suma cyfr jest równa 24, to mamy 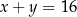 , czyli
, czyli 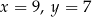 lub odwrotnie. Mamy więc w tym przypadku dwie liczby:
lub odwrotnie. Mamy więc w tym przypadku dwie liczby: 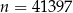 lub
lub 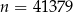 .
.
Jest więc 5 liczb spełniających warunki zadania:
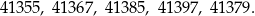
Sposób II
Skoro 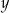 ma być cyfrą nieparzystą, więc musi być jedną z cyfr: 5, 7, 9.
ma być cyfrą nieparzystą, więc musi być jedną z cyfr: 5, 7, 9.
Jeżeli 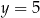 , to mamy liczbę postaci
, to mamy liczbę postaci 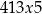 o sumie cyfr
o sumie cyfr 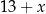 . Liczba ta jest podzielna przez 3 tylko dla
. Liczba ta jest podzielna przez 3 tylko dla 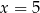 i
i 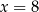 .
.
Jeżeli 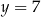 , to mamy liczbę postaci
, to mamy liczbę postaci 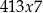 o sumie cyfr
o sumie cyfr 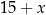 . Liczba ta jest podzielna przez 3 tylko dla
. Liczba ta jest podzielna przez 3 tylko dla 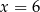 i
i 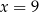 .
.
Jeżeli 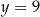 , to mamy liczbę postaci
, to mamy liczbę postaci 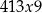 o sumie cyfr
o sumie cyfr 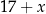 . Liczba ta jest podzielna przez 9 tylko dla
. Liczba ta jest podzielna przez 9 tylko dla 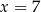 .
.
Jest więc 5 liczb spełniających warunki zadania:
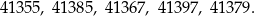
Odpowiedź: 41355, 41367, 41385, 41397, 41379

