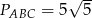Zadanie nr 5840255
W trójkącie 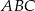 dane są
dane są 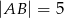 ,
, 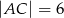 oraz iloczyn skalarny
oraz iloczyn skalarny 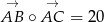 . Oblicz miarę kąta
. Oblicz miarę kąta 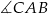 oraz pole tego trójkąta.
oraz pole tego trójkąta.
Rozwiązanie
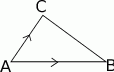
Ponieważ

to mamy
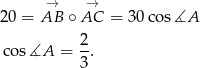
Aby obliczyć pole trójkąta potrzebujemy wyliczyć 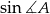 .
.
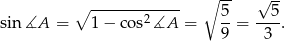
Mamy stąd
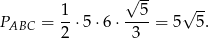
Odpowiedź: 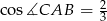 ,
, 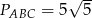
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 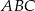 dane są
dane są 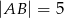 ,
, 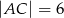 oraz iloczyn skalarny
oraz iloczyn skalarny 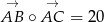 . Oblicz miarę kąta
. Oblicz miarę kąta 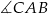 oraz pole tego trójkąta.
oraz pole tego trójkąta.

Ponieważ

to mamy
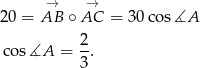
Aby obliczyć pole trójkąta potrzebujemy wyliczyć 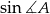 .
.
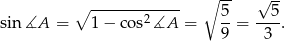
Mamy stąd
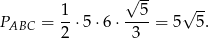
Odpowiedź: 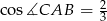 ,
,