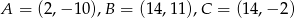Zadanie nr 6347587
Punkt 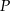 jest punktem wspólnym przekątnych trapezu
jest punktem wspólnym przekątnych trapezu 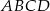 , w którym
, w którym 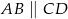 oraz
oraz ![−→ −→ −→ D = (1 0,− 9),AB = [12,21],CB = [0,13],CP = [− 3,− 2]](https://img.zadania.info/zad/6347587/HzadT3x.gif) . Oblicz współrzędne pozostałych wierzchołków trapezu
. Oblicz współrzędne pozostałych wierzchołków trapezu 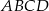 .
.
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
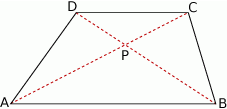
Zauważmy, że trójkąty 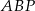 i
i 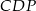 są podobne (mają równe kąty) – oznaczmy skalę ich podobieństwa przez
są podobne (mają równe kąty) – oznaczmy skalę ich podobieństwa przez 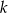 . Zauważmy, że z podanych wektorów możemy wyliczyć
. Zauważmy, że z podanych wektorów możemy wyliczyć 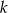 . Rzeczywiście, wiemy, że
. Rzeczywiście, wiemy, że
![−→ −→ −→ CA = CB + BA = [0,13]+ [− 12 ,−2 1] = [− 12 ,−8 ].](https://img.zadania.info/zad/6347587/HzadR5x.gif)
Zatem
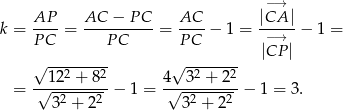
W takim razie
![−→ 1-−→ 1- DC = 3AB = 3[12,2 1] = [4,7 ].](https://img.zadania.info/zad/6347587/HzadR7x.gif)
To z kolei pozwala wyliczyć współrzędne punktu 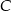 .
.
![−→ [4,7] = DC = [xc − 10,yc + 9] ⇒ C = (14,− 2).](https://img.zadania.info/zad/6347587/HzadR9x.gif)
Teraz wyliczamy współrzędne punktów 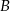 i
i 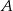 .
.
![−→ [0,13] = CB = [xb − 14,yb + 2 ] ⇒ B = (14,11 ) −→ [12,21] = AB = [14− xa,11 − ya] ⇒ A = (2,− 10).](https://img.zadania.info/zad/6347587/HzadR12x.gif)
Odpowiedź: