Zadanie nr 9753089
Punkty 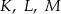 są środkami boków
są środkami boków 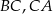 i
i 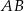 trójkąta
trójkąta 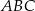 . Wykaż, że
. Wykaż, że
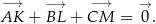
Rozwiązanie
Zaczynamy od rysunku.
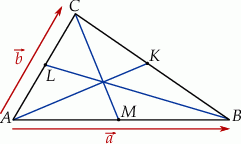
Spróbujemy wyznaczyć wektory 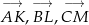 w zależności od wektorów utworzonych z boków trójkąta.
w zależności od wektorów utworzonych z boków trójkąta.
Sposób I
Oznaczmy 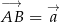 oraz
oraz 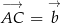 . Mamy wtedy
. Mamy wtedy
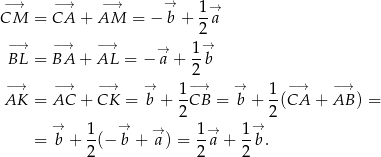
Mamy zatem
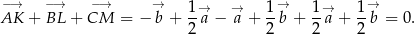
Sposób II
Liczymy
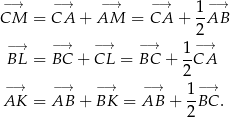
Mamy zatem
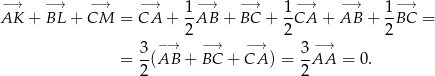
Sposób III
Umieśćmy trójkąt 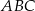 w układzie współrzędnych tak, aby
w układzie współrzędnych tak, aby 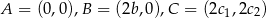 .
.
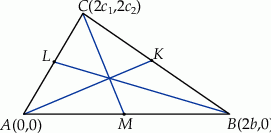
Mamy wtedy
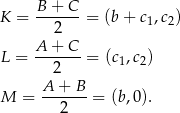
Zatem
![A−K→ + −B→L + C−M→ = [b + c ,c ]+ [c − 2b,c ]+ [b − 2c ,− 2c ] = [0,0]. 1 2 1 2 1 2](https://img.zadania.info/zad/9753089/HzadR12x.gif)
Sposób IV
Liczymy utożsamiając działania na punktach z działaniami na wektorach.