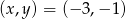/Szkoła średnia/Równania/Układy równań/Liniowy

Zadanie nr 3343897

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż algebraicznie i graficznie układ równań 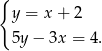{ y = x+ 2 5y − 3x = 4.

Rozwiązanie

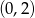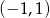Zacznijmy od rozwiązania graficznego. Musimy narysować obie proste będące wykresami równań układu. Aby to zrobić, dla każdego z równań znajdujemy dwa spełniające go punkty, potem prowadzimy proste przez te punkty. Nie jest to trudne, dla pierwszego równania możemy np. wziąć (0,2) i (− 1,1) . Żeby znaleźć ładne punkty dla drugiego równania, zapiszmy je w postaci 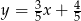3 4 y = 5x + 5 . 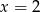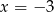Podstawiamy teraz x = 2 i x = −3 i dostajemy punkty 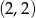(2 ,2 ) i (− 3,− 1) .

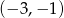Rysujemy teraz obie proste i zgadujemy z wykresu punkt wspólny: 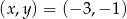(x,y ) = (− 3,− 1) .

PIC

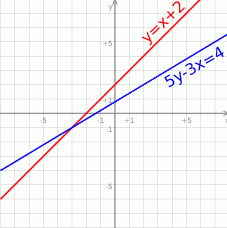
Na koniec należy sprawdzić, czy liczby te rzeczywiście spełniają oba równania – trzeba to sprawdzić, bo mogliśmy mieć niedokładny wykres.

Rozwiążmy teraz układ algebraicznie. Podstawiając z pierwszego równania 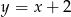y = x+ 2 do drugiego, mamy

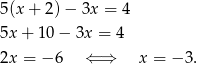
5 (x+ 2)− 3x = 4 5x + 10− 3x = 4 2x = − 6 ⇐ ⇒ x = − 3.

Z pierwszego równania mamy więc 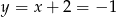y = x + 2 = − 1 .  
Odpowiedź: (x,y) = (− 3,− 1)

Wersja PDF