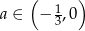Zadanie nr 9471812
Dla jakich wartości parametru  układ równań
układ równań 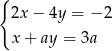 ma rozwiązanie będące parą liczb o różnych znakach?
ma rozwiązanie będące parą liczb o różnych znakach?
Rozwiązanie
Sposób I
Nie przejmujemy się parametrem i rozwiązujemy podany układ równań. Dzielimy pierwsze równanie przez 2 i odejmujemy od niego drugie (żeby skrócić  ).
).
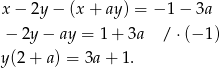
Jeżeli teraz 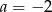 , to powyższe równanie jest sprzeczne. W takim razie musi być
, to powyższe równanie jest sprzeczne. W takim razie musi być 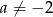 i mamy
i mamy
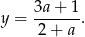
Mamy wtedy (z pierwszego równania układu)
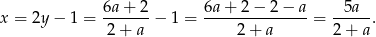
Jeżeli rozwiązania mają być różnych znaków, to musi być spełniona nierówność
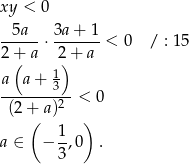
Mogliśmy też osobno sprawdzić kiedy 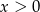 i
i 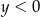 lub
lub 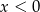 i
i 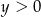 .
.
Sposób II
Podany układ
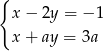
wygodnie jest rozwiązać metodą wyznacznikową
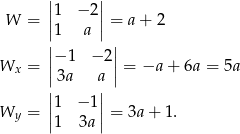
To oznacza, że układ jest sprzeczny dla 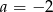 , a w przeciwnym przypadku mamy
, a w przeciwnym przypadku mamy
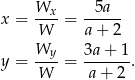
Dalej rozwiązujemy tak jak w poprzednim sposobie.
Odpowiedź: