/Szkoła średnia/Równania/Układy równań/Liniowy

Zadanie nr 9866700

Dodaj do ulubionych
Dodaj do rozwiązanych

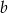Podaj te wartości a , przy których dla każdego b istnieje takie c , że układ równań:

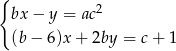
{ bx− y = ac2 (b− 6 )x+ 2by = c + 1

ma zawsze przynajmniej jedno rozwiązanie.

Rozwiązanie

Treść trochę pokręcona, ale nie przejmujmy się, tylko spróbujmy rozwiązać ten układ równań. Skorzystamy z metody wyznacznikowej. Liczymy wyznaczniki

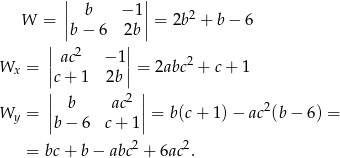
| | W = || b − 1|| = 2b 2 + b − 6 |b − 6 2b| || 2 || Wx = | ac − 1|= 2abc2 + c+ 1 |c+ 1 2b | || b ac2 || Wy = || || = b(c+ 1)− ac2(b− 6) = b − 6 c+ 1 = bc+ b− abc2 + 6ac2.

Sprawdźmy jeszcze kiedy wyznacznik główny jest równy 0.

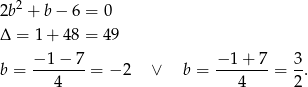
2b2 + b− 6 = 0 Δ = 1+ 48 = 49 − 1 − 7 − 1 + 7 3 b = ------- = − 2 ∨ b = ------- = -. 4 4 2

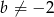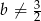Widać zatem, że dla b ⁄= − 2 i b ⁄= 3 2 układ ma zawsze dokładnie jedno rozwiązanie (niezależnie od wartości a i c ). Pozostało zbadać co się dzieje w pozostałych dwóch przypadkach.

Załóżmy najpierw, że 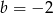b = − 2 . Mamy wtedy

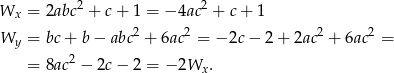
2 2 Wx = 2abc + c + 1 = − 4ac + c + 1 Wy = bc + b − abc2 + 6ac2 = − 2c − 2 + 2ac2 + 6ac2 = 2 = 8ac − 2c − 2 = −2Wx .

Aby teraz układ miał co najmniej jedno rozwiązanie, oba wyznaczniki muszą być równe 0. Pytanie zatem brzmi: dla jakich wartości a równanie

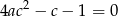
4ac2 − c− 1 = 0

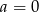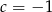ma rozwiązanie? Jeżeli a = 0 to c = − 1 jest rozwiązaniem. Jeżeli natomiast 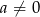a ⁄= 0 to liczymy 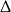Δ -ę

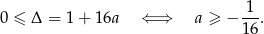
-1- 0 ≤ Δ = 1 + 16a ⇐ ⇒ a ≥ − 16.

Teraz sprawdzamy co się dzieje dla 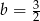b = 32 . Mamy wtedy

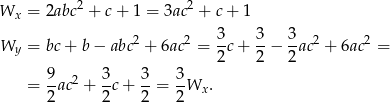
Wx = 2abc2 + c+ 1 = 3ac2 + c+ 1 3 3 3 Wy = bc+ b − abc 2 + 6ac 2 =-c + --− -ac2 + 6ac2 = 2 2 2 = 9ac2 + 3-c+ 3-= 3-W . 2 2 2 2 x

Tak jak poprzednio, musimy sprawdzić, kiedy równanie

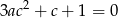
3ac2 + c+ 1 = 0

ma rozwiązanie. Dla 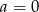a = 0 mamy rozwiązanie 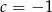c = − 1 . Jeżeli 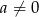a ⁄= 0 to liczymy 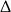Δ -ę.

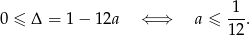
0 ≤ Δ = 1− 12a ⇐ ⇒ a ≤ -1. 12

Ostatecznie mamy 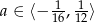-1 -1 a ∈ ⟨− 16,12⟩ .  
Odpowiedź: a ∈ ⟨− 116,112⟩

Wersja PDF