/Szkoła średnia/Równania/Układy równań/Liniowy

Zadanie nr 9984269

Dodaj do ulubionych
Dodaj do rozwiązanych

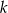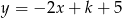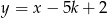Podaj dla jakich wartości parametru k punkt przecięcia się wykresów funkcji y = − 2x+ k+ 5 i y = x − 5k + 2 należy do koła o środku 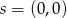s = (0,0 ) i promieniu r = 3 .

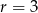Rozwiązanie

Zacznijmy od znalezienia punktu wspólnego podanych prostych, czyli od rozwiązania układu równań

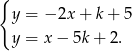
{ y = − 2x + k + 5 y = x − 5k + 2.

Dodajmy do pierwszego równania dwa razy drugie (żeby skrócić x )

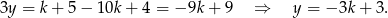
3y = k+ 5− 10k + 4 = − 9k + 9 ⇒ y = − 3k+ 3.

Zatem z drugiego równania

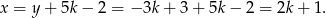
x = y + 5k − 2 = − 3k + 3 + 5k − 2 = 2k+ 1.

Koło, o którym mowa, jest opisane nierównością

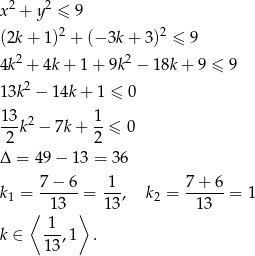
2 2 x + y ≤ 9 (2k + 1 )2 + (− 3k + 3)2 ≤ 9 2 2 4k + 4k + 1 + 9k − 1 8k+ 9 ≤ 9 1 3k2 − 14k+ 1 ≤ 0 13k2 − 7k + 1-≤ 0 2 2 Δ = 49 − 13 = 36 k = 7−--6-= 1-, k = 7+--6-= 1 1 ⟨ 13 ⟩ 13 2 13 1 k ∈ ---,1 . 1 3

 
Odpowiedź: ⟨ 1 ⟩ k ∈ 13,1

Wersja PDF