/Szkoła średnia/Geometria/Stereometria/Sześcian

Zadanie nr 1029671

Dodaj do ulubionych
Dodaj do rozwiązanych

Po wydłużeniu każdej krawędzi sześcianu o 2, długość jego przekątnej podwoiła się. Oblicz pole powierzchni całkowitej powiększonego sześcianu.

Rozwiązanie

Zaczynamy od rysunku

PIC

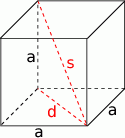
Długość przekątnej podstawy jest dana wzorem

√ -- d = a 2.

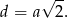
Zatem na mocy twierdzenia Pitagorasa, przekątna sześcianu jest dana wzorem

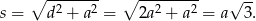
∘ -------- ∘ --------- √ -- s = d2 + a2 = 2a 2 + a 2 = a 3.

Korzystamy z założenia i otrzymujemy równanie

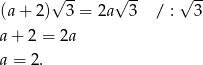
√ -- √ -- √ -- (a + 2) 3 = 2a 3 / : 3 a + 2 = 2a a = 2 .

Pole powierzchni powiększonego sześcianu jest więc równe

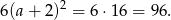
6(a + 2)2 = 6⋅16 = 96.

 
Odpowiedź: 96

Wersja PDF