Zadanie nr 1288735
Wykaż, że w sześcianie, odległość krawędzi od nieprzecinającej się z nią przekątnej sześcianu jest równa połowie długości przekątnej ściany.
Rozwiązanie
Zróbmy szkicowy rysunek.
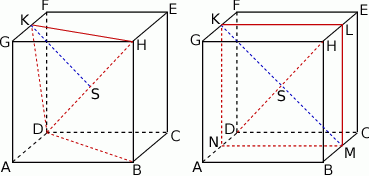
Musimy znaleźć odcinek, który jest jednocześnie prostopadły do 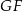 i
i 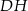 . Twierdzimy, że taką własność ma odcinek
. Twierdzimy, że taką własność ma odcinek 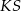 łączący środek krawędzi
łączący środek krawędzi 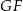 ze środkiem przekątnej
ze środkiem przekątnej 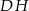 .
.
Jest on prostopadły do 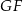 , bo leży w płaszczyźnie prostopadłej do
, bo leży w płaszczyźnie prostopadłej do 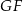 i przechodzącej przez środek krawędzi
i przechodzącej przez środek krawędzi 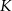 . Z drugiej, strony trójkąt
. Z drugiej, strony trójkąt 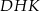 jest równoramienny, więc jego środkowa
jest równoramienny, więc jego środkowa 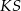 jest jednocześnie jego wysokością, czyli
jest jednocześnie jego wysokością, czyli 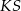 jest prostopadły do
jest prostopadły do 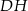 .
.
Sposób I
Obliczymy długość odcinka 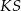 z trójkąta prostokątnego
z trójkąta prostokątnego 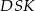 .
.
Ponieważ skala nie jest istotna, możemy założyć, że krawędź sześcianu ma długość 1. Długość przekątnej 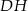 sześcianu liczymy z trójkąta prostokątnego
sześcianu liczymy z trójkąta prostokątnego 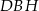
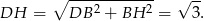
Zatem
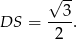
Podobnie, z twierdzenia Pitagorasa w trójkącie 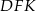 , obliczmy długość odcinka
, obliczmy długość odcinka 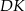
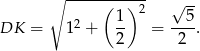
Możemy teraz obliczyć długość odcinka 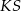 .
.
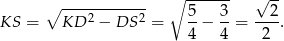
Jest to oczywiście dokładnie połowa długości przekątnej ściany sześcianu.
Sposób II
Zauważmy, że ponieważ punkt 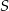 jest środkiem sześcianu, punkt ten jest jednocześnie środkiem kwadratu
jest środkiem sześcianu, punkt ten jest jednocześnie środkiem kwadratu 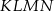 , którego wierzchołki są środkami krawędzi
, którego wierzchołki są środkami krawędzi 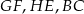 i
i 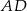 . Zatem
. Zatem 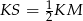 jest połową przekątnej kwadratu
jest połową przekątnej kwadratu 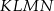 . Kwadrat ten jest przystający do kwadratu
. Kwadrat ten jest przystający do kwadratu 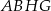 , co dowodzi, że odcinek
, co dowodzi, że odcinek 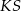 ma długość równą połowie przekątnej ściany sześcianu.
ma długość równą połowie przekątnej ściany sześcianu.

