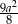/Szkoła średnia/Geometria/Stereometria/Sześcian

Zadanie nr 4174794

Dodaj do ulubionych
Dodaj do rozwiązanych

Krawędź sześcianu ma długość a . Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

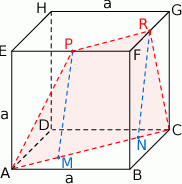
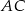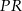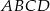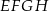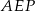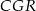Po pierwsze zauważmy, że odcinki AC i PR są równoległe (jako odcinki wspólne równoległych płaszczyzn ABCD i EF GH oraz płaszczyzny cięcia). Otrzymany czworokąt jest więc trapezem. Jest to w dodatku trapez równoramienny, bo trójkąty AEP i CGR są przystające. Obliczmy długości podstaw i ramion tego trapezu.

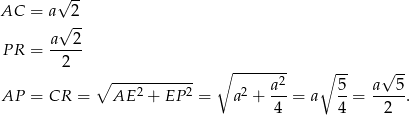
√ -- AC = a√ 2- a 2 P R = ----- 2 ∘ -------- ∘ -- √ -- ∘ ----2-----2 2 a2- 5- a--5- AP = CR = AE + EP = a + 4 = a 4 = 2 .

Wysokość trapezu obliczamy z trójkąta prostokątnego 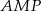AMP .

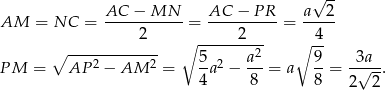
√ -- AC − MN AC − P R a 2 AM = NC = -----------= ----------= ----- 2 ∘ -----2--- ∘ -4 ∘ ---2-------2- 5-2 a2- 9- -3a-- PM = AP − AM = 4a − 8 = a 8 = 2√ 2-.

Pozostało obliczyć pole trapezu.

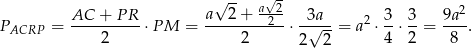
√- a√ 2-+ a-2- 2 PACRP = AC--+--PR-⋅ PM = --------2--⋅ -3√a--= a2 ⋅ 3-⋅ 3-= 9a-. 2 2 2 2 4 2 8

 
Odpowiedź: 9a2 8

Wersja PDF