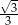/Szkoła średnia/Geometria/Stereometria/Sześcian

Zadanie nr 5526143

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.

Rozwiązanie

Zaczynamy od rysunku.

PIC

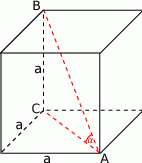
Żądany sinus wyliczymy z trójkąta prostokątnego 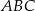ABC , ale najpierw musimy wyliczyć długości boków tego trójkąta. Mamy

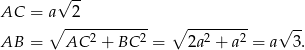
√ -- AC = a 2 ∘ ------------ ∘ --------- √ -- AB = AC 2 + BC 2 = 2a2 + a2 = a 3.

Zatem szukany sinus jest równy

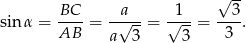
√ -- BC-- --a-- -1-- --3- sinα = AB = a√ 3 = √ 3 = 3 .

 
Odpowiedź: - √-3 3

Wersja PDF