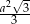/Szkoła średnia/Geometria/Stereometria/Sześcian

Zadanie nr 6719206

Dodaj do ulubionych
Dodaj do rozwiązanych

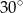Sześcian o krawędzi a przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem 30 ∘ . Oblicz pole powstałego przekroju.

Rozwiązanie

Zaczynamy od rysunku.

PIC

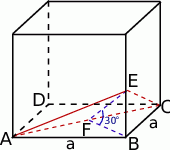
Otrzymany przekrój jest trójkątem równoramiennym o podstawie 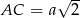√ -- AC = a 2 . Wyliczymy jego wysokość 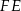FE . Patrząc na trójkąt prostokątny 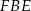F BE mamy

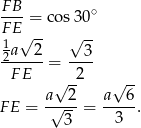
FB- ∘ FE = cos3 0 1 √ -- √ -- 2a--2-= --3- FE -2 a√ 2 a√ 6- F E = √----= ----. 3 3

Zatem pole wynosi

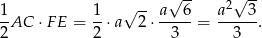
-- √ -- 2√ -- 1-AC ⋅ FE = 1-⋅a√ 2 ⋅ a-6-= a---3. 2 2 3 3

 
Odpowiedź: 2√- a--3 3

Wersja PDF