/Szkoła średnia/Geometria/Stereometria/Sześcian

Zadanie nr 7546342

Dodaj do ulubionych
Dodaj do rozwiązanych

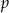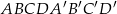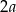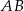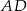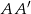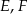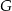Płaszczyzna p jest styczna do kuli wpisanej w sześcian ′ ′ ′ ′ ABCDA B C D o krawędzi długości 2a oraz przecina krawędzie AB , AD i AA ′ w takich punktach E ,F i G odpowiednio, że 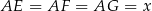AE = AF = AG = x . Wykonaj odpowiedni rysunek i wyznacz x .

PIC

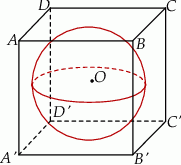
Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

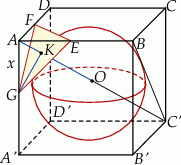
Łatwo jest obliczyć wysokość 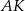AK ostrosłupa 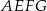AEF G – jest to różnica między długością połowy przekątnej sześcianu a promieniem kuli wpisanej. Długość przekątnej 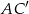AC ′ możemy wyliczyć np. z trójkąta prostokątnego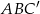 ′ ABC

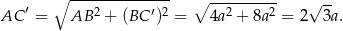
-------------- ′ ∘ 2 ′ 2 ∘ --2-----2- √ -- AC = AB + (BC ) = 4a + 8a = 2 3a.

Mamy zatem

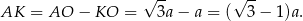
√ -- √ -- AK = AO − KO = 3a− a = ( 3 − 1)a.

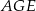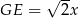Z trójkąta prostokątnego AGE mamy √ -- GE = 2x . Zatem ze wzoru na wysokość w trójkącie równobocznym mamy

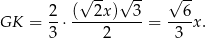
√ -- √ -- √ -- 2 ( 2x) 3 6 GK = -⋅ ----------= ---x . 3 2 3

Stosujemy teraz twierdzenie Pitagorasa w trójkącie 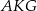AKG

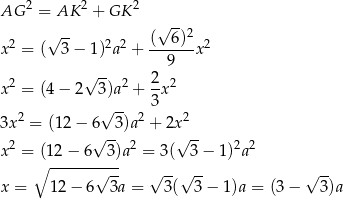
2 2 2 AG = AK + GK √ -- 2 √ -- 2 2 ( 6)2 2 x = ( 3− 1) a + ------x √ -- 9 x 2 = (4− 2 3)a2 + 2x 2 √ -- 3 3x 2 = (12 − 6 3)a2 + 2x 2 √ -- √ -- x 2 = (12− 6 3)a2 = 3( 3− 1 )2a2 ∘ ------√--- √ --√ -- √ -- x = 12 − 6 3a = 3( 3 − 1)a = (3 − 3)a

 
Odpowiedź: ---------- ∘ √ -- √ -- x = 12 − 6 3a = (3− 3)a

Wersja PDF