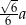Zadanie nr 7654508
Oblicz odległość środka ściany sześcianu o krawędzi długości  od przekątnej tego sześcianu.
od przekątnej tego sześcianu.
Rozwiązanie
Szkicujemy sześcian.
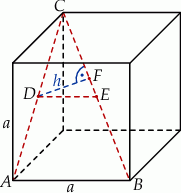
Na powyższym rysunku  jest środkiem ściany sześcianu (a więc też środkiem odcinka
jest środkiem ściany sześcianu (a więc też środkiem odcinka  ),
), 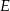 jest środkiem sześcianu (a więc środkiem przekątnej
jest środkiem sześcianu (a więc środkiem przekątnej 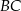 ), a
), a 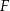 jest rzutem punktu
jest rzutem punktu 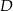 na przekątną
na przekątną 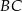 . Zadanie sprowadza się do obliczenia długości wysokości
. Zadanie sprowadza się do obliczenia długości wysokości 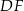 w trójkącie prostokątnym
w trójkącie prostokątnym 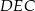 .
.
Sposób I
Trójkąty 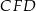 i
i 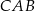 są oba prostokątne oraz mają wspólny kąt ostry przy wierzchołku
są oba prostokątne oraz mają wspólny kąt ostry przy wierzchołku 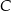 . Są więc podobne. Korzystamy z tego podobieństwa i mamy
. Są więc podobne. Korzystamy z tego podobieństwa i mamy
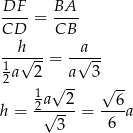
Sposób II
Obliczamy pole trójkąta 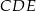 na dwa sposoby.
na dwa sposoby.
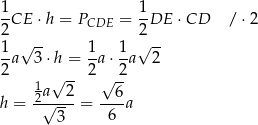
Odpowiedź: