Zadanie nr 7752506
Ania bawi się sześciennymi klockami o krawędzi 2 cm i buduje z nich bryły w kształcie prostokątów (prostopadłościanów o wysokości 1 klocka) w sposób przedstawiony na poniższym rysunku.
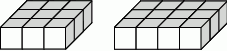
Najpierw Ania zbudowała z klocków pełen kwadrat o krawędzi 36 cm i wykorzystała do tego wszystkie swoje klocki. Następnie zburzyła tę budowlę i ułożyła z tych klocków prostokąt. Wtedy okazało się, że został jej dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej z ułożonych figur do pola powierzchni całkowitej drugiej figury.
Rozwiązanie
Wiemy, że do ułożenia kwadratu o krawędzi 36 cm Ania zużyła wszystkie swoje klocki, więc miała ich
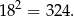
Po ułożeniu prostokąta został jej jeden klocek, więc ułożyła go z
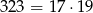
klocków. Ponieważ 17 i 19 są liczbami pierwszymi utworzony prostokąt musiał mieć wymiary 17 na 19 klocków (nie mógł być paskiem pojedynczych klocków, bo mamy informację o tym, że 324 klocka nie było gdzie dołożyć).
Pole powierzchni pierwszego utworzonego kwadratu składa się z
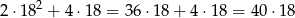
kwadratów o krawędzi 2 (po 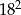 na podstawach i
na podstawach i 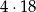 na obwodzie).
na obwodzie).
Pole powierzchni utworzonego później prostokąta składa się z
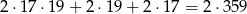
kwadratów o krawędzi 2 (po 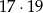 na podstawach i
na podstawach i 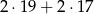 na obwodzie).
na obwodzie).
Stosunek pól powierzchni jest więc równy
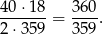
Odpowiedź: