Zadanie nr 5527540
Dany jest sześcian 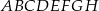 . Przez wierzchołki
. Przez wierzchołki 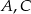 oraz
oraz 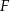 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 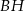 w punkcie
w punkcie 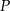 (zobacz rysunek).
(zobacz rysunek).
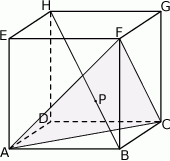
Wykaż, że 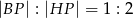 .
.
Rozwiązanie
Niech 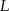 będzie środkiem podstawy sześcianu.
będzie środkiem podstawy sześcianu.
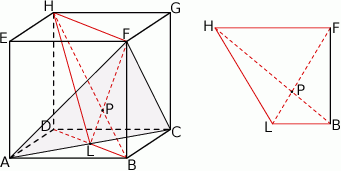
Interesujący nas punkt 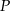 jest punktem wspólnym przekątnych
jest punktem wspólnym przekątnych 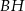 i
i 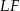 trapezu prostokątnego
trapezu prostokątnego 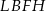 , w którym
, w którym 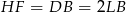 . Korzystamy teraz z podobieństwa trójkątów
. Korzystamy teraz z podobieństwa trójkątów 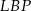 i
i 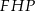 .
.