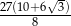/Szkoła średnia/Geometria/Stereometria/Sześcian/Objętość i pole

Zadanie nr 1993187

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekątna sześcianu jest o 3 dłuższa od krawędzi sześcianu. Oblicz objętość tego sześcianu.

Rozwiązanie

Zaczynamy od rysunku

PIC

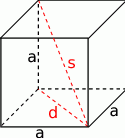
Długość przekątnej podstawy jest dana wzorem

√ -- d = a 2.

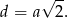
Zatem na mocy twierdzenia Pitagorasa, przekątna sześcianu jest dana wzorem

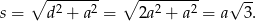
∘ -------- ∘ --------- √ -- s = d2 + a2 = 2a 2 + a 2 = a 3.

Korzystamy z założenia i otrzymujemy równanie

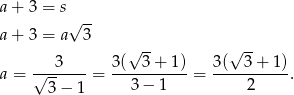
a+ 3 = s √ -- a+ 3 = a 3 √ -- √ -- 3 3( 3 + 1) 3( 3 + 1) a = √-------= -----------= ----------. 3 − 1 3− 1 2

Teraz obliczamy objętość

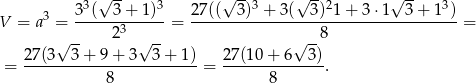
3 √ -- 3 √ --3 √ --2 √ -- 3 V = a3 = 3-(--3+--1)--= 27((--3)-+--3(--3)-1-+-3⋅-1--3+--1-)-= √ -- 23 √ -- √ --8 27(3 3 + 9 + 3 3 + 1) 27(10 + 6 3 ) = ------------------------= --------------. 8 8

 
Odpowiedź: 27(10+6√3) -----8----

Wersja PDF