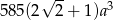/Szkoła średnia/Geometria/Stereometria/Sześcian/Objętość i pole

Zadanie nr 2741617

Dodaj do ulubionych
Dodaj do rozwiązanych

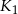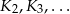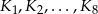Niech K1 będzie sześcianem o krawędzi długości a . Konstruujemy kolejno sześciany K2,K 3,... takie, że pole powierzchni całkowitej kolejnego sześcianu jest dwa razy większe od pola powierzchni poprzedniego sześcianu. Oblicz sumę objętości sześcianów K ,K ,...,K 1 2 8 .

Rozwiązanie

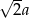Zauważmy, że jeżeli a jest długością krawędzi jednego z sześcianów, to kolejny sześcian ma krawędź długości √ -- 2a (żeby pole powierzchni wzrosło dwukrotnie).

PIC

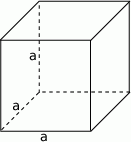
To oznacza, że ten kolejny sześcian ma objętość

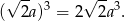
√ -- √ -- ( 2a )3 = 2 2a3.

Objętości kolejnych sześcianów tworzą więc ciąg geometryczny 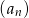(an) z pierwszym wyrazem 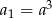a = a3 1 i ilorazem 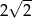√ -- 2 2 . Suma 8 początkowych wyrazów tego ciągu jest równa

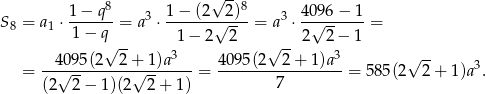
1 − q8 1 − (2 √ 2)8 4096 − 1 S8 = a1 ⋅-------= a3 ⋅------√----= a3 ⋅-√-------= 1− q√ -- 1− 2 2 √ -- 2 2 − 1 40 95(2 2 + 1)a3 4095(2 2 + 1)a3 √ -- = ---√---------√------- = -----------------= 585(2 2 + 1 )a 3. (2 2− 1)(2 2+ 1) 7

 
Odpowiedź: √ -- 3 585 (2 2+ 1)a

Wersja PDF