/Szkoła średnia/Geometria/Stereometria/Sześcian/Objętość i pole

Zadanie nr 3420912

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 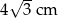√ -- 4 3 cm .

Rozwiązanie

Zacznijmy od zauważenia, że przekątna sześcianu o krawędzi a ma długość √ -- a 3 .

PIC

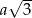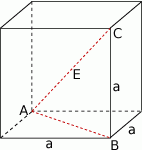
Rzeczywiście, na mocy twierdzenia Pitagorasa przekątna kwadratu w podstawie ma długość 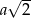√ -- a 2 i korzystając z Twierdzenia Pitagorasa w trójkącie ABC mamy

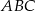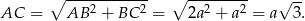
∘ ------------ ∘ --------- AC = AB 2 + BC 2 = 2a2 + a2 = a√ 3.

Mamy zatem równanie

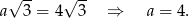
√ -- √ -- a 3 = 4 3 ⇒ a = 4.

Teraz bez trudu liczymy objętość i pole powierzchni.

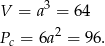
V = a3 = 64 2 Pc = 6a = 9 6.

 
Odpowiedź: Objętość 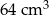64 cm 3 , pole powierzchni: 2 96 cm

Wersja PDF