Zadanie nr 5771844
Punkty 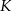 i
i 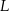 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 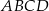 i krawędzi
i krawędzi 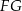 sześcianu
sześcianu 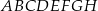 . Suma kwadratów długości odcinków
. Suma kwadratów długości odcinków 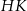 i
i 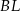 jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.
jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.
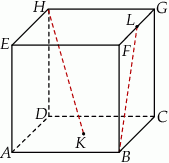
Rozwiązanie
Oznaczmy długość krawędzi sześcianu przez  .
.
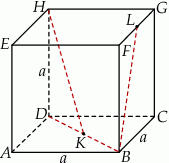
Obliczamy długości odcinków 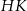 i
i 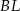 w zależności od
w zależności od  , tak aby móc wykorzystać podaną informację o sumie kwadratów długości tych odcinków.
, tak aby móc wykorzystać podaną informację o sumie kwadratów długości tych odcinków.
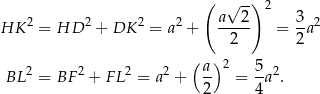
Mamy zatem
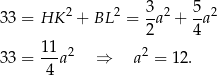
Pole powierzchni całkowitej sześcianu jest więc równe
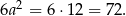
Odpowiedź: 72

