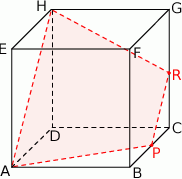
Dany jest sześcian 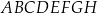 o krawędzi długości
o krawędzi długości  . Punkt
. Punkt 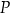 jest środkiem krawędzi
jest środkiem krawędzi 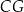 tego sześcianu.
tego sześcianu.
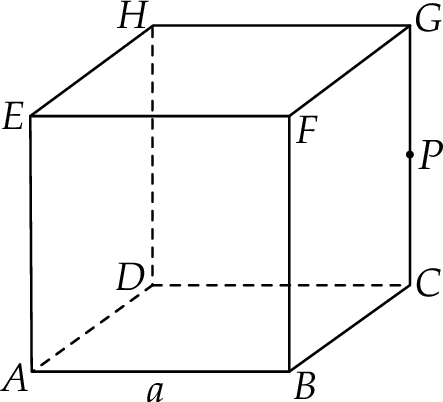
Oblicz odległość wierzchołka 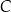 od płaszczyzny zawierającej punkty
od płaszczyzny zawierającej punkty 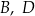 oraz
oraz 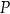 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest sześcian 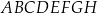 o krawędzi długości
o krawędzi długości  . Punkt
. Punkt 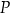 jest środkiem krawędzi
jest środkiem krawędzi 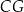 tego sześcianu.
tego sześcianu.

Oblicz odległość wierzchołka 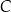 od płaszczyzny zawierającej punkty
od płaszczyzny zawierającej punkty 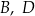 oraz
oraz 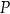 .
.
Przez środek jednej krawędzi podstawy sześcianu, koniec przeciwległej krawędzi tej podstawy oraz środek krawędzi bocznej, poprowadzono płaszczyznę. Opisz figurę, którą otrzymamy w wyniku tego przekroju. Rozważ 2 przypadki.
Krawędź sześcianu ma długość  . Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.
. Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.
Sześcian przecięto płaszczyzną przechodzącą przez przekątną podstawy. Płaszczyzna ta tworzy z podstawą kąt  . Dla jakich wartości
. Dla jakich wartości 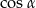 otrzymany przekrój jest trójkątem?
otrzymany przekrój jest trójkątem?
Sześcian o krawędzi  przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem 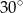 . Oblicz pole powstałego przekroju.
. Oblicz pole powstałego przekroju.
Przez środki trzech różnych krawędzi sześcianu 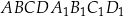 wychodzących z wierzchołka
wychodzących z wierzchołka 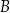 poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt
poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt 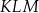 . Oblicz odległość wierzchołka
. Oblicz odległość wierzchołka 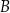 od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.
od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.
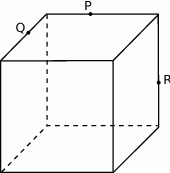
Narysuj przekrój równoległościanu płaszczyzną 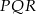 .
.
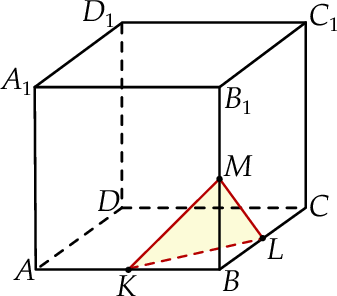
Dany jest sześcian 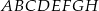 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 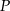 jest środkiem krawędzi
jest środkiem krawędzi 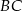 . Płaszczyzna
. Płaszczyzna 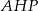 przecina krawędź
przecina krawędź 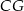 w punkcie
w punkcie 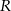 (zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty
(zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty 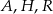 i
i 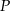 .
.