/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1020205

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie 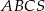ABCS podstawa 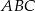ABC jest trójkątem prostokątnym, 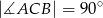|∡ACB | = 90∘ . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość 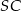SC ostrosłupa ma długość 24 cm. Oblicz:

  • objętość ostrosłupa;
  • tangens kąta nachylenia ściany bocznej ostrosłupa, zawierającej przeciwprostokątną podstawy, do płaszczyzny podstawy.

Rozwiązanie

Zaczynamy naturalnie od rysunku.

PIC

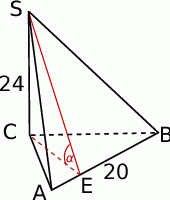
  • Ponieważ promień okręgu opisanego na trójkącie prostokątnym, to połowa przeciwprostokątnej, to 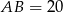AB = 20 . Powiedzmy, że 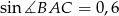sin ∡BAC = 0 ,6 . Mamy wtedy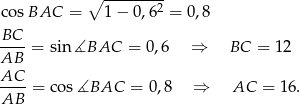
    ∘ --------- co sBAC = 1 − 0,6 2 = 0,8 BC ----= sin ∡BAC = 0,6 ⇒ BC = 12 AB AC--= cos ∡BAC = 0 ,8 ⇒ AC = 1 6. AB

    Zatem objętość ostrosłupa jest równa

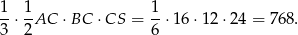
    1 1 1 --⋅--AC ⋅BC ⋅ CS = --⋅16 ⋅12⋅ 24 = 768 . 3 2 6

     
    Odpowiedź: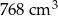 7 68 cm 3

  • Wiemy, że 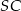SC jest wysokością ostrosłupa, zatem płaszczyzna przechodząca przez tę krawędź oraz przez wysokość 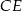CE trójkąta 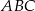ABC jest prostopadła do krawędzi 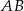AB . Zatem kąt nachylenia ściany 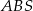ABS do płaszczyzny podstawy to kąt 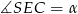∡SEC = α . Aby obliczyć jego tangens, wyliczmy wysokość 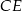CE trójkąta 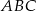ABC . Ze wzoru na pole trójkąta mamy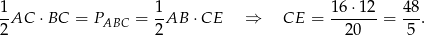
    1 1 16 ⋅12 48 -AC ⋅BC = PABC = -AB ⋅CE ⇒ CE = -------= --. 2 2 20 5

    Zatem szukany tangens jest równy

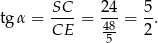
    SC-- 24- 5- tg α = CE = 48 = 2 . 5

     
    Odpowiedź: 5 2

Wersja PDF