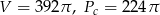Zadanie nr 1221017
Tworząca stożka ma długość 25, a średnica podstawy stożka jest krótsza od wysokości stożka o 10. Oblicz pole powierzchni całkowitej i objętość tego stożka.
Rozwiązanie
Szkicujemy stożek.
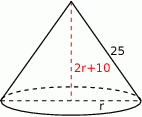
Jeżeli przez  oznaczymy długość promienia podstawy, to wysokość stożka
oznaczymy długość promienia podstawy, to wysokość stożka 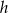 spełnia warunek
spełnia warunek 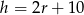 . Korzystamy teraz z twierdzenia Pitagorasa.
. Korzystamy teraz z twierdzenia Pitagorasa.
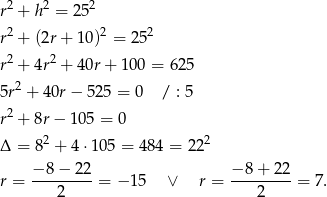
Ujemne rozwiązanie odrzucamy i mamy 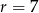 . Stąd
. Stąd 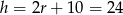 . Pozostało obliczyć objętość i pole powierzchni całkowitej.
. Pozostało obliczyć objętość i pole powierzchni całkowitej.
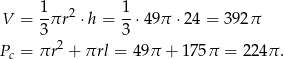
Odpowiedź: