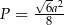/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1310540

Dodaj do ulubionych
Dodaj do rozwiązanych

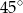Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa a . Kąt między krawędzią boczną i krawędzią podstawy ma miarę 4 5∘ . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

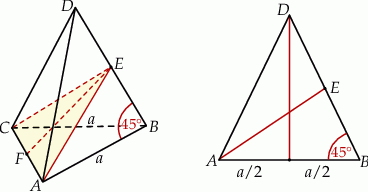
Jeżeli popatrzymy na trójkąt równoramienny 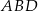ABD , to widać, że łatwo można obliczyć krawędź boczną:

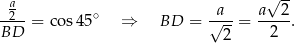
√ -- -a2-- ∘ --a- a--2- BD = cos45 ⇒ BD = √ 2-= 2 .

Inny sposób wyliczenia 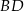BD , to zauważenie, że 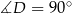∡D = 90 ∘ i zastosowanie twierdzenia Pitagorasa.

Teraz patrzymy na trójkąt 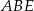ABE , korzystając z twierdzenia cosinusów możemy obliczyć długość odcinka AE .

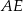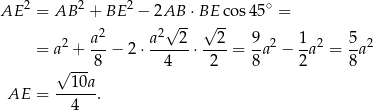
AE 2 = AB 2 + BE 2 − 2AB ⋅ BE cos 45∘ = 2 2√ -- √ -- = a2 + a--− 2⋅ a---2-⋅--2-= 9a2 − 1-a2 = 5-a2 √ ---8 4 2 8 2 8 10a AE = ------. 4

Prostszy sposób wyliczenia 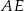AE , to skorzystanie z równości 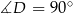∡D = 90∘ i zastosowanie twierdzenia Pitagorasa do trójkąta AED .

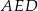Teraz już łatwo, z trójkąta prostokątnego 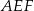AEF wyliczymy długość wysokości 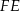FE i wtedy już łatwo policzymy pole.

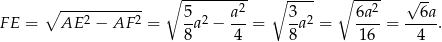
∘ --------- ∘ ---- ∘ ---- √ -- ∘ ---2------2- 5-2 a2- 3- 2 6a2- --6a- F E = AE − AF = 8a − 4 = 8 a = 16 = 4 .

Pozostało policzyć pole.

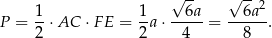
√ -- √ -- 1 1 6a 6a2 P = --⋅AC ⋅F E = --a⋅ -----= -----. 2 2 4 8

 
Odpowiedź: - √-6a2 P = 8

Wersja PDF