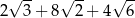/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1330167

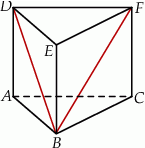
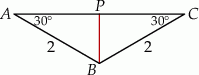
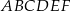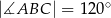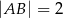Podstawą graniastosłupa prostego ABCDEF jest trójkąt ABC , w którym |∡ABC | = 120∘ oraz |AB | = 2 (zobacz rysunek). Trójkąt 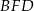BF D jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.

PIC

Wersja PDF

Rozwiązanie

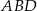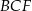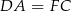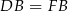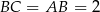Zauważmy najpierw, że trójkąty prostokątne ABD i BCF mają dwa takie same boki: DA = FC i DB = FB . To oznacza, że trójkąty te są przystające i BC = AB = 2 .

PIC

Niech 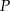P będzie środkiem odcinka 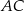AC . Z trójkąta prostokątnego 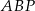ABP mamy

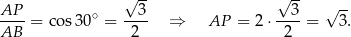
√ -- √ -- AP-- ∘ --3- --3- √ -- AB = cos30 = 2 ⇒ AP = 2 ⋅ 2 = 3.

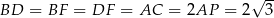Zatem √ -- BD = BF = DF = AC = 2AP = 2 3 . Patrzymy teraz na trójkąt prostokątny ABD .

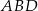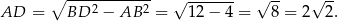
∘ ------------ -- -- AD = BD 2 − AB 2 = √ 12−--4 = √ 8 = 2√ 2.

Liczymy teraz pole powierzchni całkowitej.

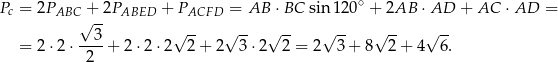
Pc = 2PABC + 2PABED + PACFD = AB ⋅BC sin 120∘ + 2AB ⋅AD + AC ⋅ AD = √ -- = 2 ⋅2⋅ --3-+ 2 ⋅2⋅ 2√ 2+ 2√ 3⋅ 2√ 2-= 2√ 3-+ 8√ 2-+ 4√ 6. 2

 
Odpowiedź: √ -- √ -- √ -- 2 3 + 8 2 + 4 6

Wersja PDF