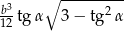/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1342790

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 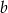b , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę α . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Zaczynamy od rysunku.

PIC

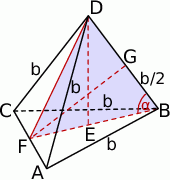
Łatwo obliczyć wysokość ostrosłupa. Z trójkąta 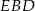EBD mamy

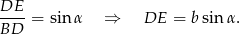
DE--= sin α ⇒ DE = bsin α. BD

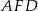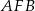Aby wyliczyć jakieś odcinki w podstawie zauważmy, że trójkąty AF D i AF B są przystające. Zatem 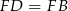F D = FB i trójkąt 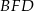BF D jest równoramienny. Z trójkąta 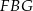F BG możemy obliczyć długość odcinka FB .

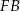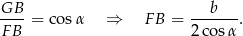
GB-- = cos α ⇒ F B = ---b---. FB 2 cos α

Teraz z trójkąta prostokątnego 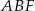ABF obliczamy AF .

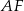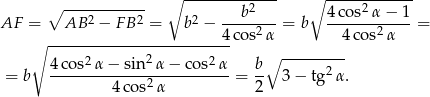
∘ ------------- ∘ ------------ ∘ ----2-----2 2 --b-2--- 4-cos2α-−-1- AF = AB − F B = b − 4co s2α = b 4 cos2α = ∘ ------------------------- --------- 4-cos2-α−--sin-2α-−-cos2-α b-∘ 2 = b 4co s2α = 2 3 − tg α .

Zatem objętość jest równa

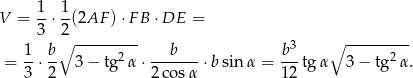
1 1 V = --⋅-(2AF )⋅F B ⋅DE = 3 2∘ --------- ∘ --------- 1- b- 2 ---b--- b3- 2 = 3 ⋅2 3 − tg α ⋅2 cos α ⋅bsin α = 12 tgα 3 − tg α .

 
Odpowiedź: ∘ --------- b3 tg α 3− tg 2α 12

Wersja PDF