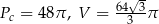/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1407930

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekrój osiowy stożka jest trójkątem równobocznym o polu 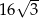√ -- 16 3 . Oblicz objętość i pole powierzchni całkowitej tego stożka.

Rozwiązanie

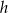Szkicujemy stożek. Oznaczmy przez r promień jego podstawy, a przez h jego wysokość.

PIC

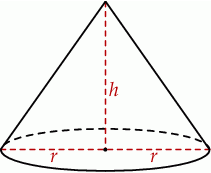
Z podanego pola przekroju mamy

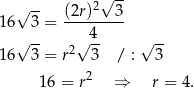
2√ -- 16√ 3-= (2r)---3- 4 16√ 3-= r2√ 3- / : √ 3 16 = r2 ⇒ r = 4.

Liczymy teraz pole powierzchni całkowitej stożka.

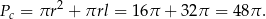
Pc = πr 2 + πrl = 16π + 32π = 48π .

Zanim obliczymy objętość, obliczamy wysokość stożka – korzystamy ze wzoru na wysokość trójkąta równobocznego.

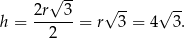
-- 2r√ 3 √ -- √ -- h = ------= r 3 = 4 3. 2

Pozostało obliczyć objętość stożka.

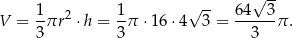
1 1 √ -- 64 √ 3- V = -πr 2 ⋅h = -π ⋅16⋅ 4 3 = ------π . 3 3 3

 
Odpowiedź: 64√3 Pc = 48π, V = --3--π

Wersja PDF