Zadanie nr 1499052
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna o długości 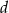 tworzy z wysokością kąt o mierze
tworzy z wysokością kąt o mierze  .
.
- Wyprowadź wzór na objętość walca.
- Oblicz tę objętość dla
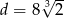 i
i 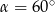 .
.
Rozwiązanie
Zaczynamy od rysunku.
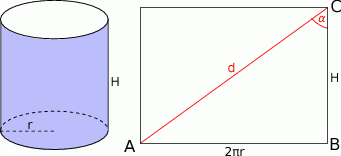
Po rozwinięciu powierzchni bocznej walca, otrzymamy prostokąt o bokach długości 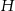 i
i 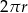 , gdzie
, gdzie  jest promieniem podstawy walca.
jest promieniem podstawy walca.
- Patrząc na trójkąt
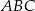 mamy
mamy 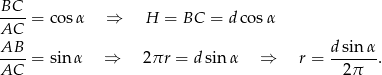
Liczymy teraz objętość walca.
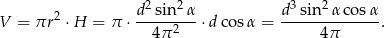
Odpowiedź: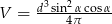
- Podstawiamy we wzorze z poprzedniego podpunktu podane dane.
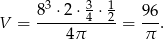
Odpowiedź: