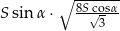/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1500836

Dodaj do ulubionych
Dodaj do rozwiązanych

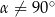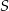W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę r wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna r z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze α ⁄= 90∘ . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę r jest równe S . Oblicz objętość graniastosłupa.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

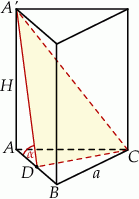
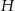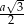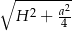Oznaczmy przez a i H długości krawędzi podstawy i wysokości graniastosłupa. Opisany przekrój jest trójkątem prostokątnym o przyprostokątnych długości a√3 -2-- i ∘ ------a2- H 2 + 4- . Mamy zatem

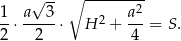
√ -- ∘ -------2- 1⋅ a--3-⋅ H 2 + a--= S. 2 2 4

Wiemy ponadto, że

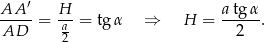
′ AA---= H- = tg α ⇒ H = a-tgα-. AD a2 2

Mamy więc

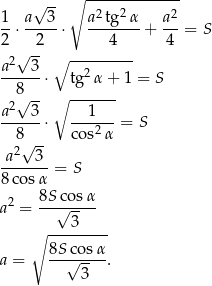
√ -- ∘ ------------- 1- a--3- a-2tg2α- a2- 2 ⋅ 2 ⋅ 4 + 4 = S √ -- ∘ --------- a2--3- 2 8 ⋅ tg α + 1 = S 2√ -- ∘ ------- a---3⋅ ---1-- = S 8√ -- cos2 α a2 3 -------= S 8cos α a2 = 8S√cosα- 3 ∘ --------- 8S-cos-α a = √ 3 .

Możemy teraz policzyć objętość

a2√ 3- a2√ 3- a tg α V = ------⋅H = ------⋅------= 4 ( 4∘ -----2--) 3√ -- 3 √ -- = a---3-tgα-= 8S-c√o-sα --3tg-α-= 8 3 8 ∘ --------- √ -- 8Sc-osα- 8S-co-sα --3-tgα- = √ 3- ⋅ √ 3- ⋅ 8 = ∘ --------- 8Sco sα = S sin α ⋅ --√-----. 3

 
Odpowiedź: ∘ ------- S sin α ⋅ 8S√cosα- 3

Wersja PDF