/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1670038

Dodaj do ulubionych
Dodaj do rozwiązanych

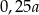Czworościan foremny o krawędzi a rozcięto płaszczyzną prostopadłą do jednej z krawędzi, przechodzącą w odległości 0,25a od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.

Rozwiązanie

Zaczynamy od rysunku.

PIC

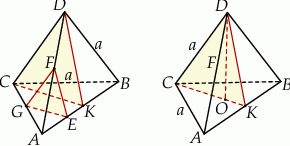
Najlepiej jest myśleć o otrzymanym przekroju 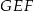GEF jak o przekroju równoległym do przekroju 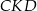CKD przechodzącego przez krawędź 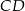CD i środek 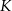K krawędzi 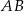AB . Ponieważ punkt 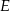E jest środkiem odcinka 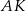AK , trójkąt 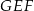GEF jest dwa razy mniejszy od trójkąta 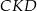CKD . Zastanówmy się jak ma się objetość czworościanu 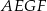AEGF do objętości wyjściowego czworościanu 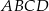ABCD . Mamy

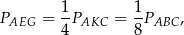
PAEG = 1PAKC = 1PABC , 4 8

oraz wysokość czworościanu 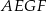AEGF jest połową wysokości czworościanu 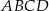ABCD . Zatem

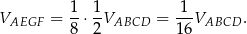
VAEGF = 1-⋅ 1VABCD = -1-VABCD . 8 2 16

No i prawie wszystko wiemy, pozostało wyliczyć objętość czworościanu foremnego 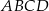ABCD .

Z polem podstawy nie ma problemu

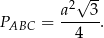
√ -- a2 3 PABC = --4---.

Wysokość 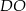DO wyliczamy z trójkąta prostokątnego 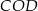COD . Ponieważ środek trójkąta równobocznego dzieli jego wysokości w stosunku 2:1 mamy

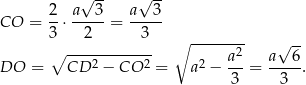
√ -- √ -- CO = 2⋅ a--3-= a--3- 3 2 3 -------- ∘ ------------ ∘ a2 a√ 6- DO = CD 2 − CO 2 = a2 − ---= ----. 3 3

Zatem objętość czworościanu jest równa

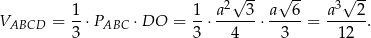
2√ -- √ -- 3√ -- VABCD = 1-⋅PABC ⋅DO = 1-⋅ a--3-⋅ a--6-= a---2. 3 3 4 3 12

Zatem

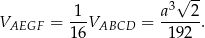
3√ -- V = 1-V = a---2-. AEGF 16 ABCD 192

Objętość pozostałej części jest równa

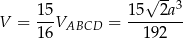
√ -- 3 V = 1-5V = 15--2a-- 1 6 ABCD 192

 
Odpowiedź: 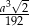3√- a1922 i √ - 3 151922a-

Wersja PDF