/Szkoła średnia/Geometria/Stereometria

Zadanie nr 1676468

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekrój ostrosłupa prawidłowego trójkątnego 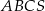ABCS płaszczyzną przechodzącą przez wierzchołek 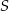S i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość 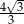√- 4-3- 3 . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

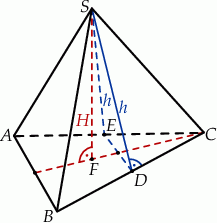
Oznaczmy przez a długość krawędzi podstawy ostrosłupa. Wtedy

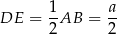
DE = 1AB = a- 2 2

(odcinek łączący środki boków w trójkącie 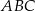ABC ). Z drugiej strony

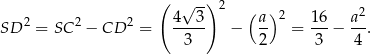
( √ --) 2 2 2 2 4--3- ( a) 2 16- a2- SD = SC − CD = 3 − 2 = 3 − 4 .

Korzystamy teraz z tego, że trójkąt 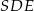SDE jest równoboczny

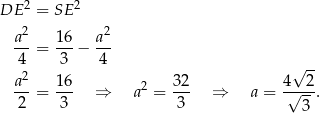
2 2 DE = SE a2 16 a2 4--= 3--− -4- 2 √ -- a--= 16- ⇒ a2 = 32- ⇒ a = 4√-2. 2 3 3 3

Mamy zatem

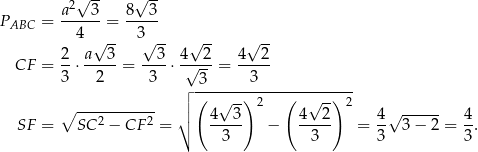
2√ -- √ -- PABC = a---3-= 8---3 4 √ -- 3√ -- √ -- √ -- 2 a 3 3 4 2 4 2 CF = -⋅ -----= ---⋅ √----= ----- 3 2 3 ┌ -3-----3-------------- ∘ ----------- ││ ( √ --)2 ( √ --) 2 SF = SC 2 − CF 2 = ∘ 4--3- − 4--2- = 4√ 3-−-2-= 4. 3 3 3 3

Objętość ostrosłupa jest więc równa

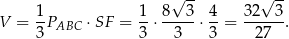
√ -- √ -- 1- 1- 8--3- 4- 32--3- V = 3 PABC ⋅SF = 3 ⋅ 3 ⋅3 = 27 .

 
Odpowiedź: √ - V = 32--3 27

Wersja PDF